Problems
Draw how Robinson Crusoe should arrange pegs and ropes so that his goat grazes in the shape of a hexagon. The hexagon doesn’t need to be regular.
Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.
One day, Robinson found a wolf in the island. He took the wolf with him and tied it with a rope to a peg. Robinson noticed that the goat would not graze anywhere that the wolf could reach. How could Robinson arrange both animals with pegs and ropes so that the goat can only graze in the shape of a waning moon? (see picture below)

Draw how Robinson Crusoe should arrange pegs, ropes, and a wolf so that the goat grazes grass in the shape of a half-ring.
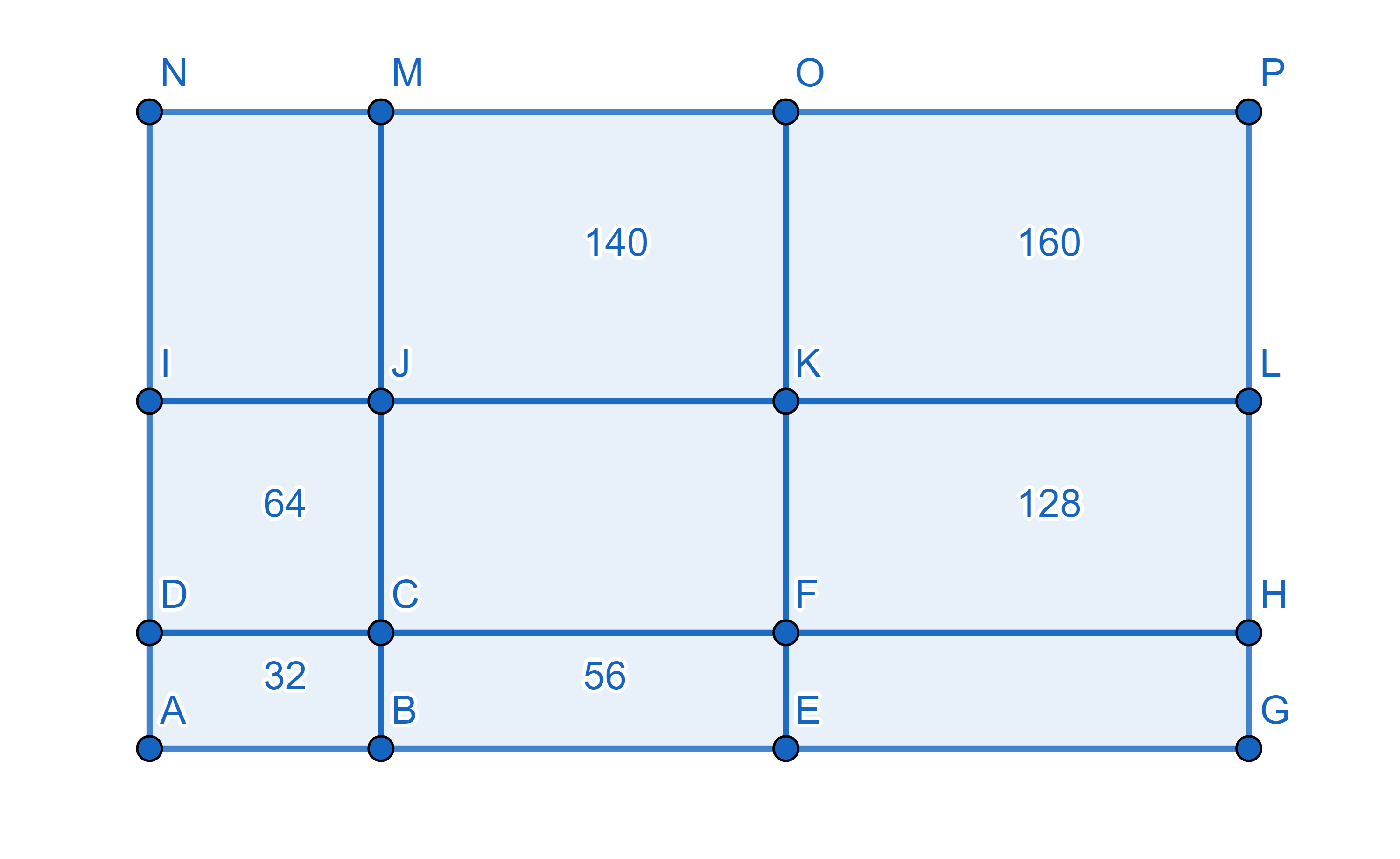
On the diagram each number denotes the area of a rectangle it is written into. What are the areas of the other rectangles?
Show how to divide any quadrilateral into \(5\) polygons of equal area.
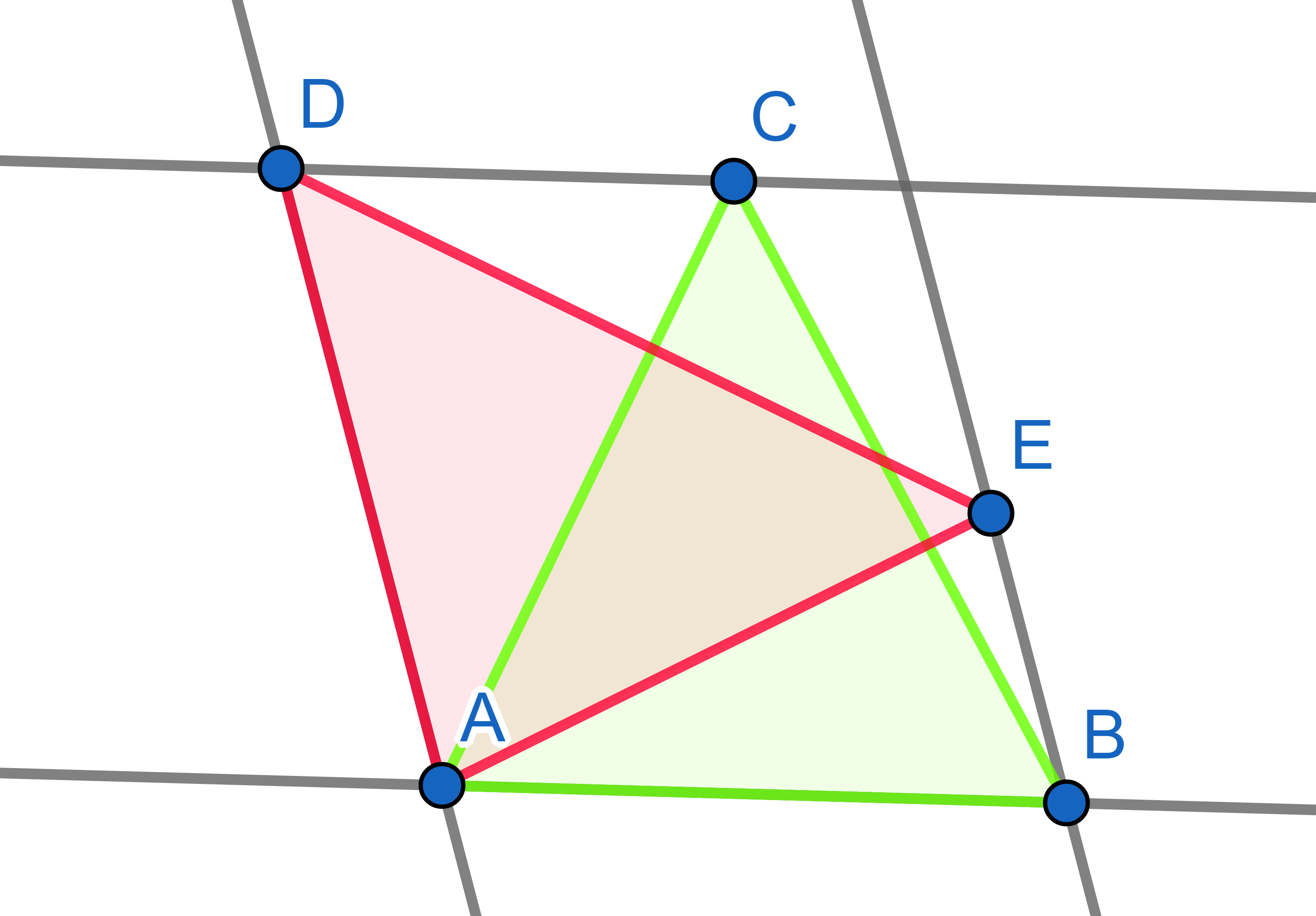
Line \(AB\) is parallel to line \(CD\) and line \(AD\) is parallel to line \(BE\). Show that triangles \(ADE\) and \(ABC\) have equal areas.
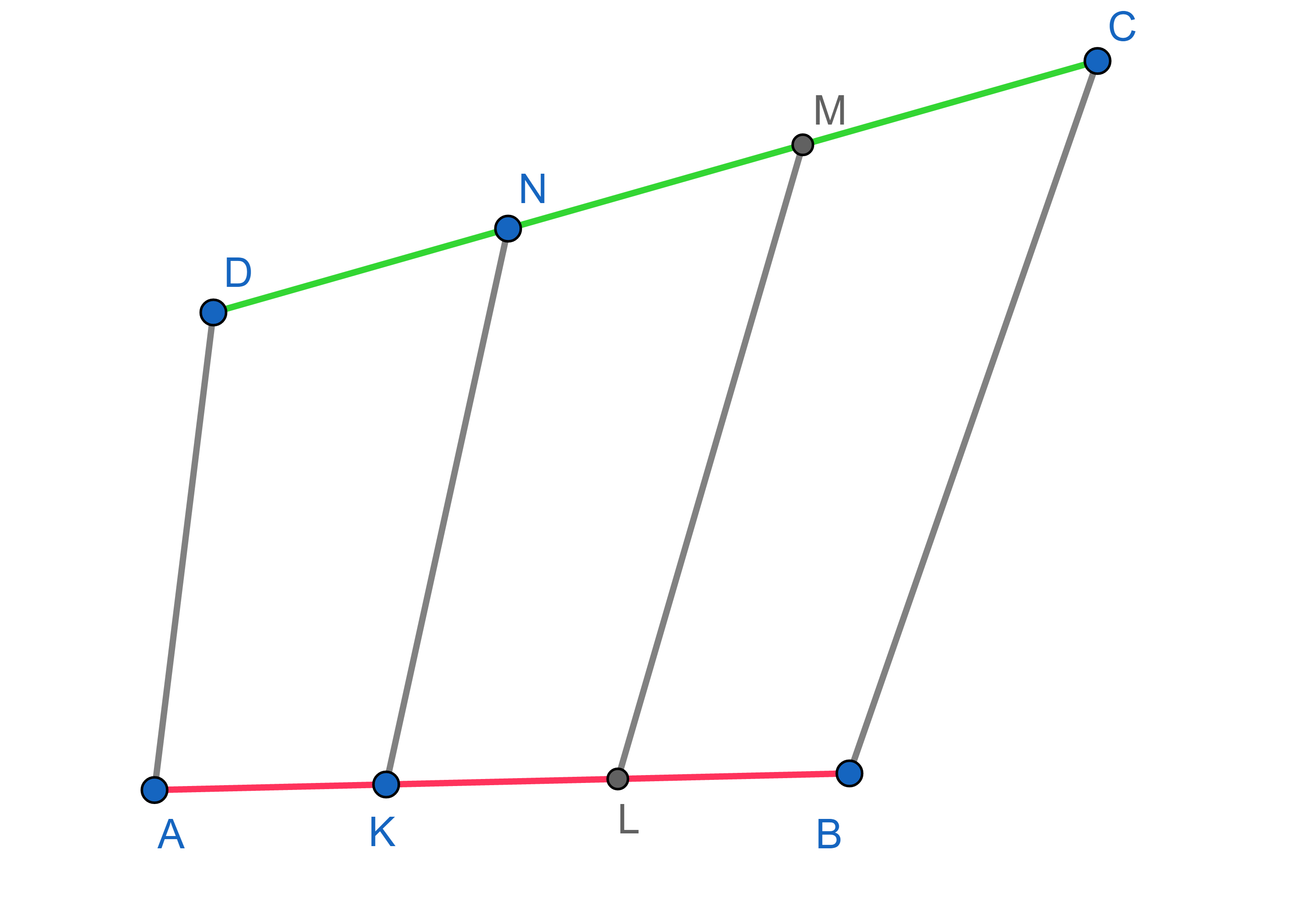
A quadrilateral \(ABCD\) is given. Points \(K\) and \(L\) belong to the side \(AB\) and \(AK=KL=LB\) and points \(N\) and \(M\) belong to the side \(CD\) and \(CM=MN=ND\). Show that the area of the quadrilateral \(KLMN\) is \(\frac13\) of the area of the quadrilateral \(ABCD\).
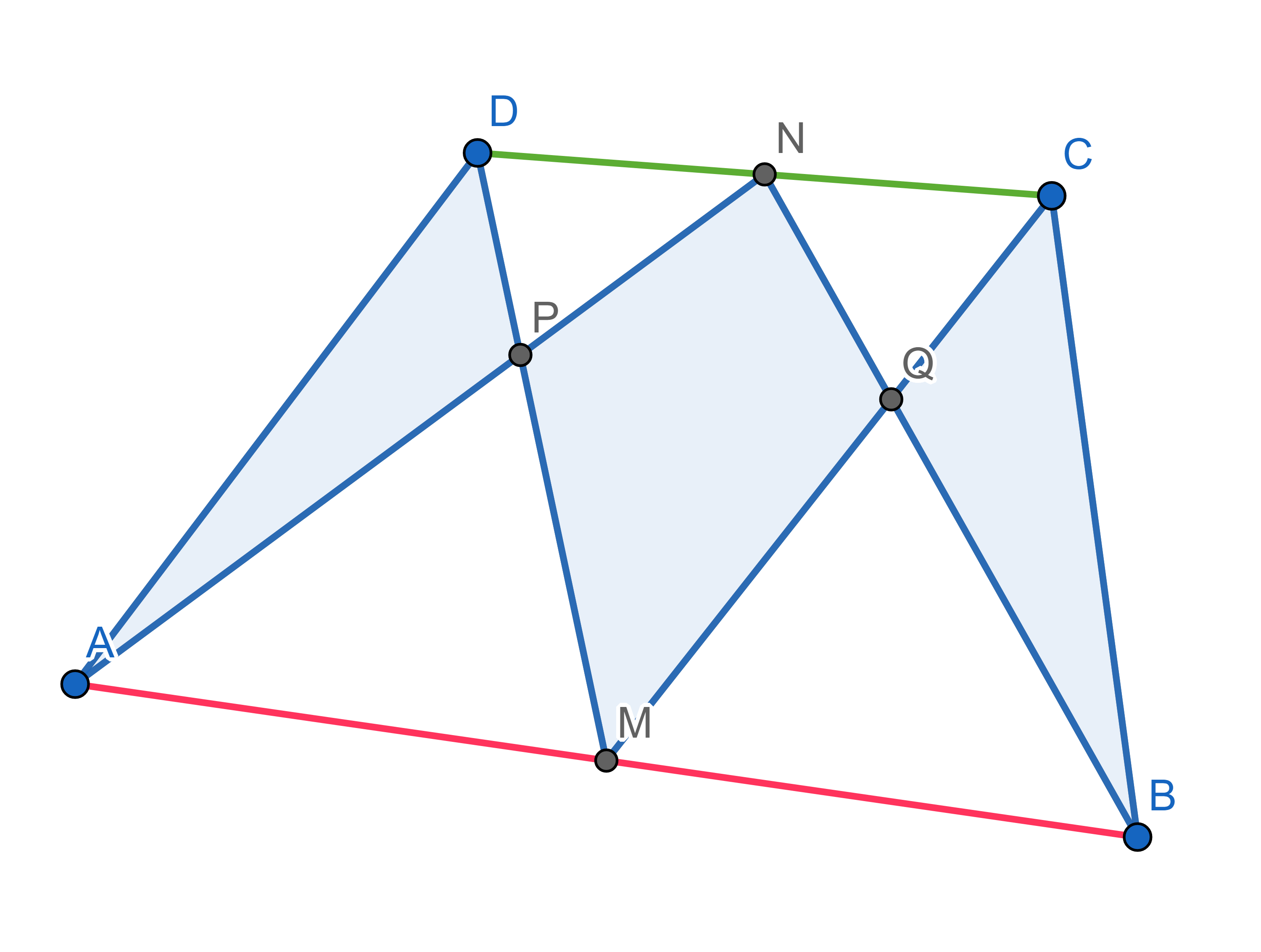
A quadrilateral \(ABCD\) is given. Point \(M\) is a midpoint of \(AB\) and point \(N\) is a midpoint of \(CD\). Point \(P\) is where segments \(AN\) and \(DM\) meet, point \(Q\) is where segments \(MC\) and \(NB\) meet. Show that the sum of the areas of triangles \(APD\) and \(BCQ\) is equal to the area of the quadrilateral \(MQNP\).
A square was cut with two parallel lines. The perpendicular distance between these two lines is \(6\)cm. One of them goes through the top right corner and the other through the bottom left corner. The three regions obtained this way, two triangles and a parallelogram, have equal areas. What is the area of the square?
