Problems

A square was cut with two parallel lines. The perpendicular distance between these two lines is \(6\)cm. One of them goes through the top right corner and the other through the bottom left corner. The three regions obtained this way, two triangles and a parallelogram, have equal areas. What is the area of the square?

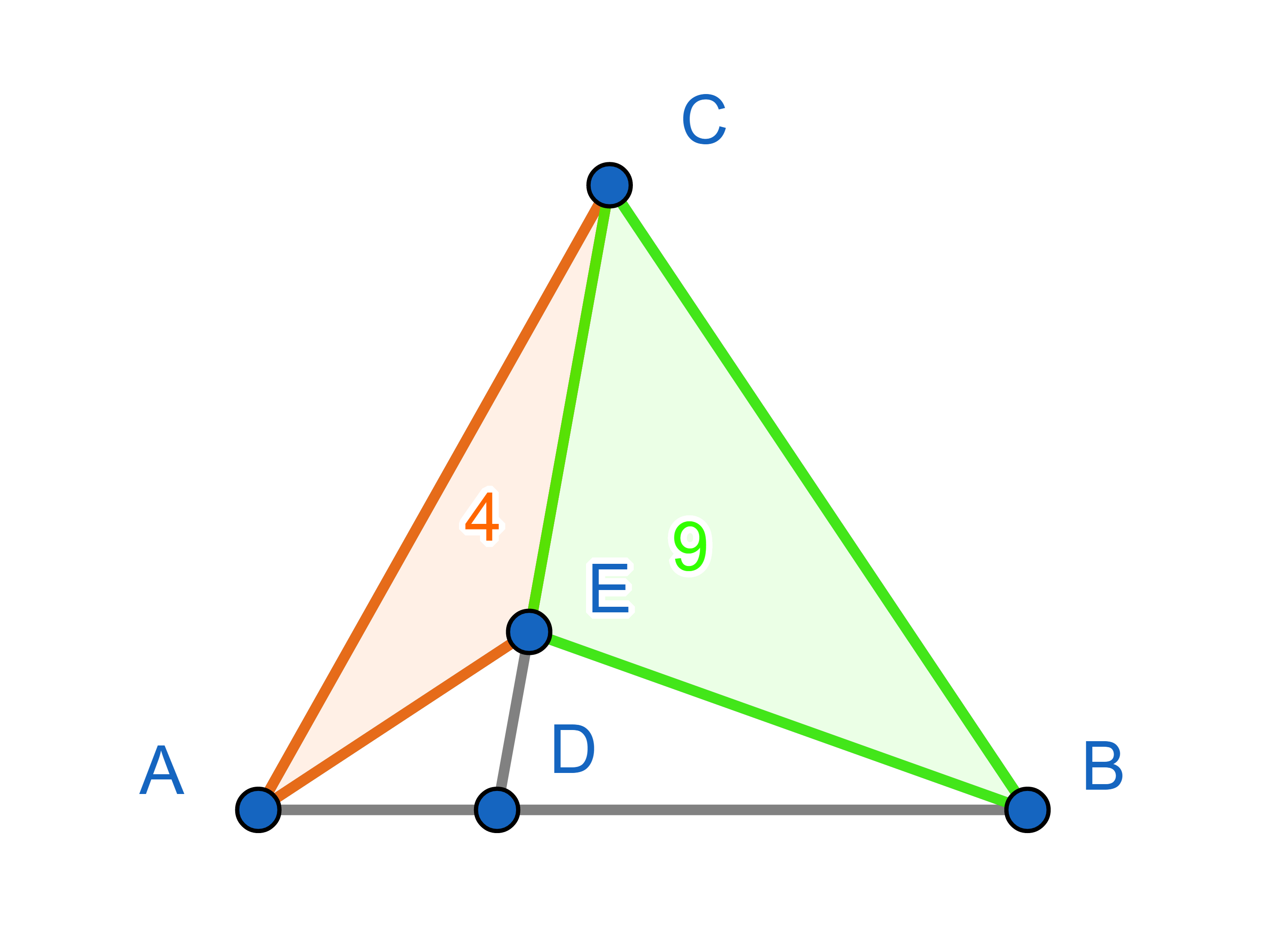
The area of the triangle \(\triangle AEC\) is \(4\), the area of the triangle \(\triangle BCE\) is \(9\) and the area of the triangle \(\triangle ABC\) is \(21\). What is the area of the triangle \(\triangle ADE\)?

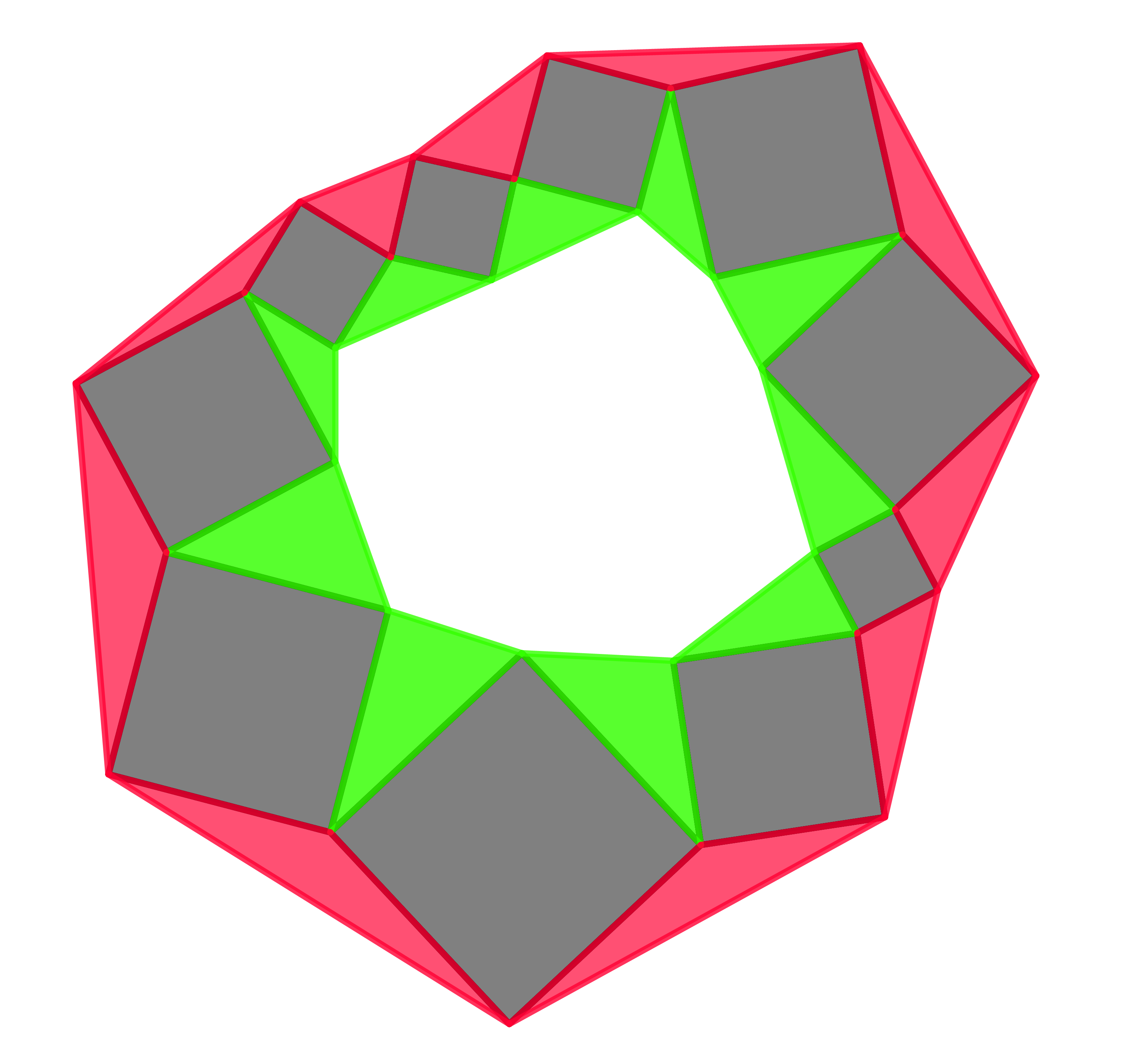
A series of squares are connected by touching vertices. Some triangles were drawn outside and inside of the chain. Show that the total green area is the same as the total red area.

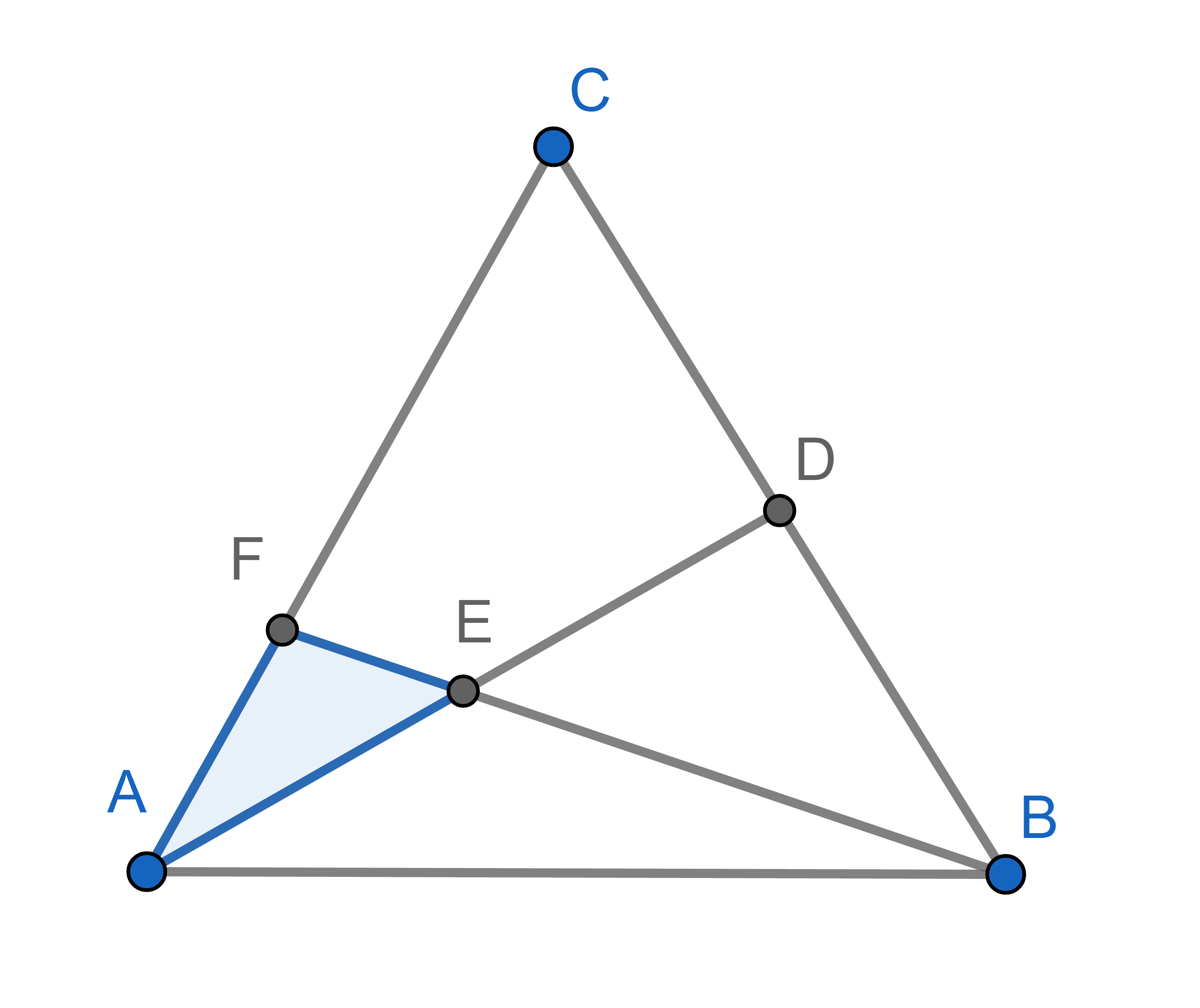
In a triangle \(\triangle ABC\), \(D\) is the midpoint of \(BC\), and \(E\) is the midpoint of \(AD\). \(F\) is the intersection of the side \(AC\) with \(BE\). What is the area of the triangle \(\triangle AEF\) as a proportion of the area of the triangle \(\triangle ABC\)?

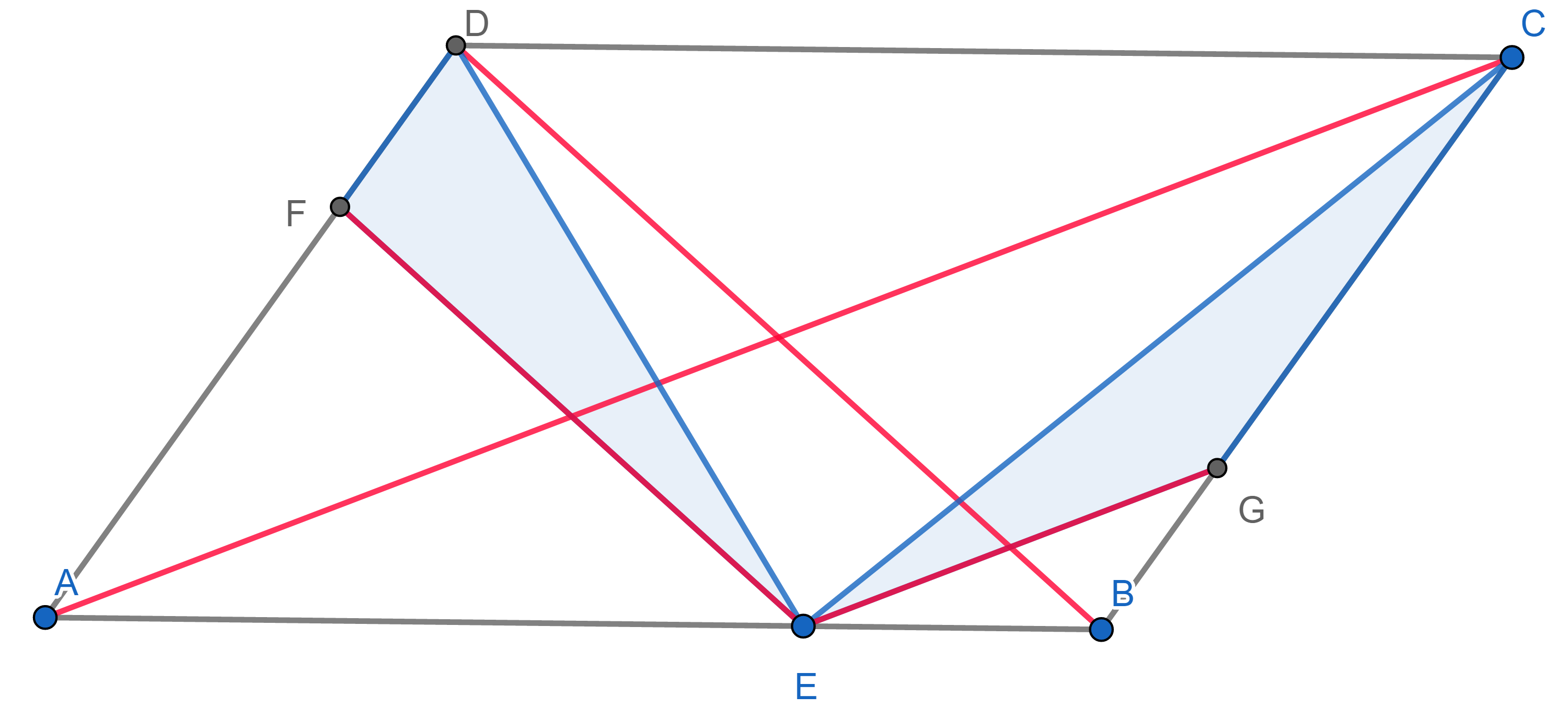
Let \(ABCD\) be a parallelogram. The segment \(EF\) is parallel to the diagonal \(BD\), and the segment \(EG\) is parallel to the diagonal \(AC\). Show that the areas of the triangles \(\triangle EFD\) and \(\triangle EGC\) are equal.

A circle is inscribed in a square, and another square is inscribed in the circle. Which area is larger, the blue or the orange one?

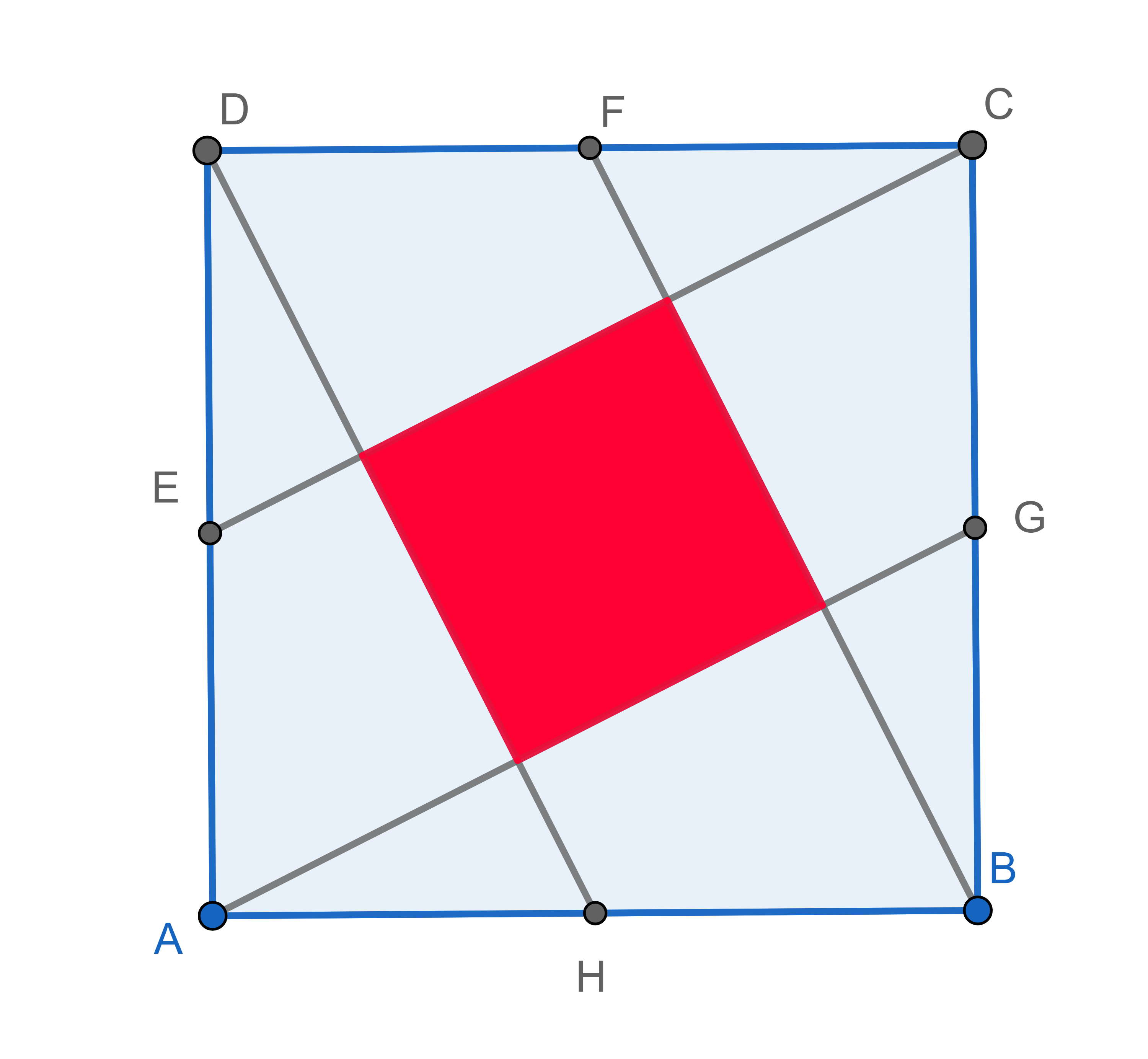
In a square, the midpoints of its sides were marked and connected to the vertices of the square. There is another square formed in the centre. The side length of the large square is \(10\). Find the area of the smaller square. (That is, the red one)

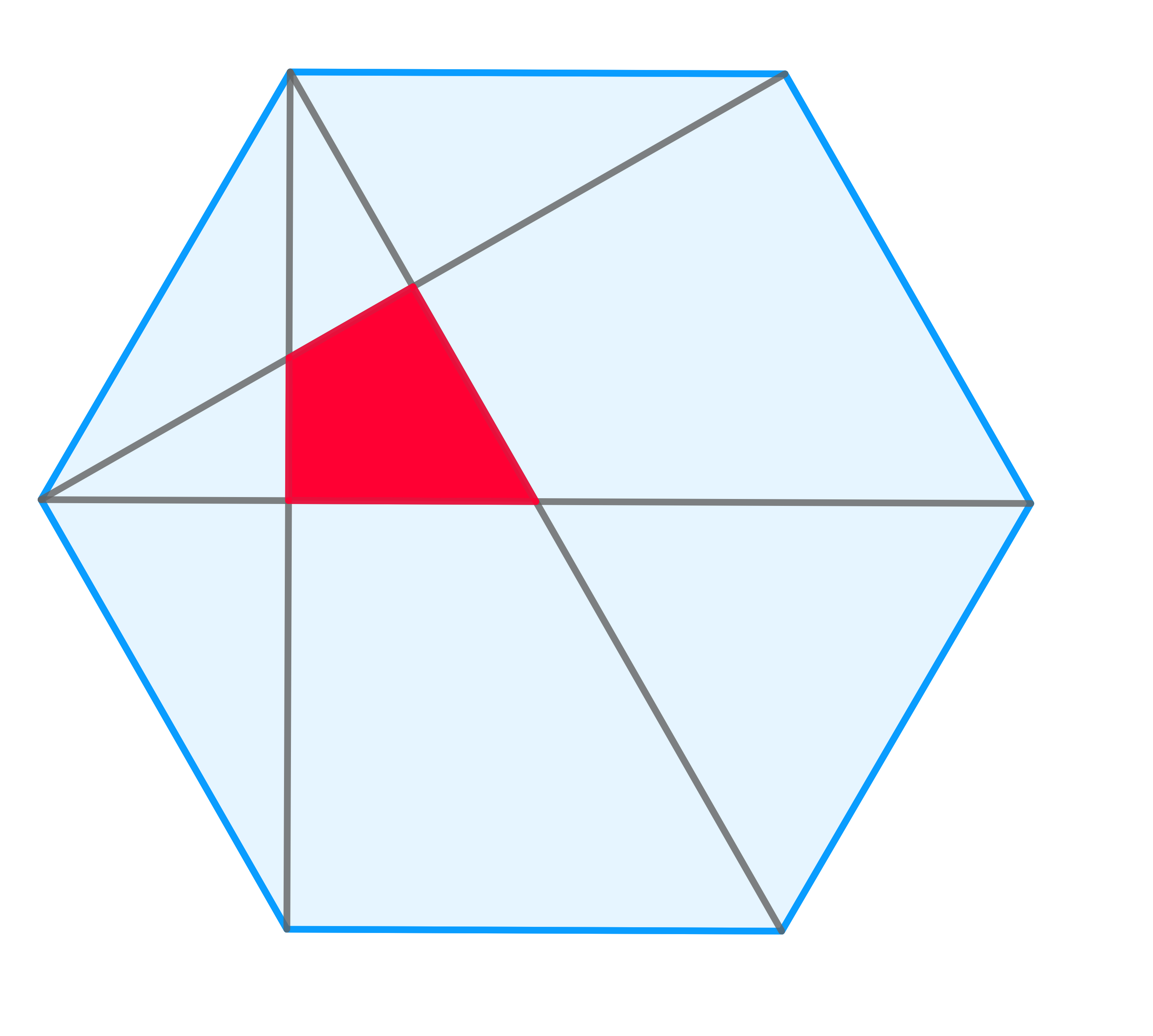
In a regular hexagon of area \(72\), some diagonals were drawn. Find the area of the red region.

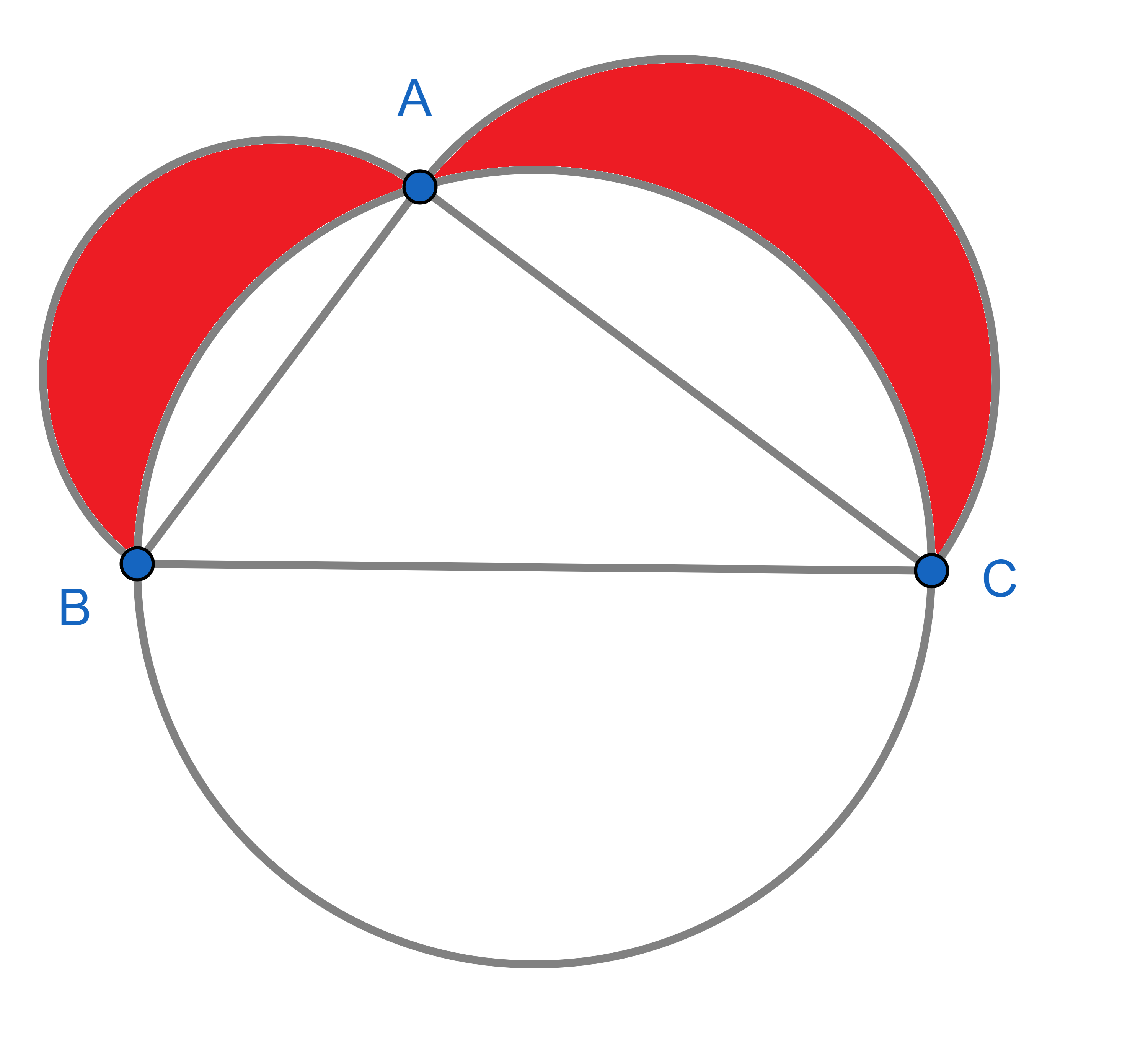
We have a triangle \(\triangle ABC\) with side lengths \(|AB|=3\), \(|AC|=4\) and angle \(\angle BAC=90^{\circ}\). A circle is drawn with side \(BC\) as diameter, and two semicircles are drawn with sides \(AB\) and \(AC\) as diameters. Find the area of the red part.

\(20\) birds fly into a photographer’s studio: \(8\) starlings, \(7\) wagtails and \(5\) woodpeckers. Each time the photographer presses the shutter to take a photograph, one of the birds flies away and does not come back. How many photographs can the photographer take to be sure that at the end there will be at least \(5\) birds of one species and at least \(3\) of another species remaining in the studio?