Problems
You and I are going to play a game. We have one million grains of sand in a bag. We take it in turns to remove \(2\), \(3\) or \(5\) grains of sand from the bag. The first person that cannot make a move loses.
Would you go first?
For every natural number \(k\ge2\), find two combinations of \(k\) real numbers such that their sum is twice their product.
Show that \(n^2+n+1\) is not divisible by \(5\) for any natural number \(n\).
Prove the following identity for any three non-zero real numbers \(a,b,c\): \[\frac{b}{2a} + \frac{c^2 + ab}{4bc} - \left|{\frac{c^2 - ab}{4bc}} \right| - \left|{\frac{b}{2a} - \frac{c^2 + ab}{4bc} + \left|{\frac{c^2 - ab}{4bc}}\right|}\right| = \min\{\frac{b}{a},\frac{c}{b},\frac{a}{c}\}.\]
There are \(n\) balls labelled 1 to \(n\). If there are \(m\) boxes labelled 1 to \(m\) containing the \(n\) balls, a legal position is one in which the box containing the ball \(i\) has number at most the number on the box containing the ball \(i+1\), for every \(i\).
There are two types of legal moves: 1. Add a new empty box labelled \(m+1\) and pick a box from box 1 to \(m+1\), say the box \(j\). Move the balls in each box with (box) number at least \(j\) up by one box. 2. Pick a box \(j\), shift the balls in the boxes with (box) number strictly greater than \(j\) down by one box. Then remove the now empty box \(m\).
Prove it is possible to go from an initial position with \(n\) boxes with the ball \(i\) in the box \(i\) to any legal position with \(m\) boxes within \(n+m\) legal moves.
Given a natural number \(n\), find a formula for the number of \(k\) less than \(n\) such that \(k\) is coprime to \(n\). Prove that the formula works.
A paper band of constant width is tied into a simple knot and tightened. Prove that the knot has the shape of a regular polygon.
In the last room, there are two doors, but someone broke into this room and the signs that used to be on the doors are now on the floor! You do not know which sign was on which door, but the statements on them say:
There is a trap behind this door.
There are traps behind both doors.
Your guide says: The first sign is true if there is treasure behind the first door, otherwise it is false. The second sign is false if there is treasure behind the second door, otherwise it is true.
But you don’t know which sign is first! What do you do?
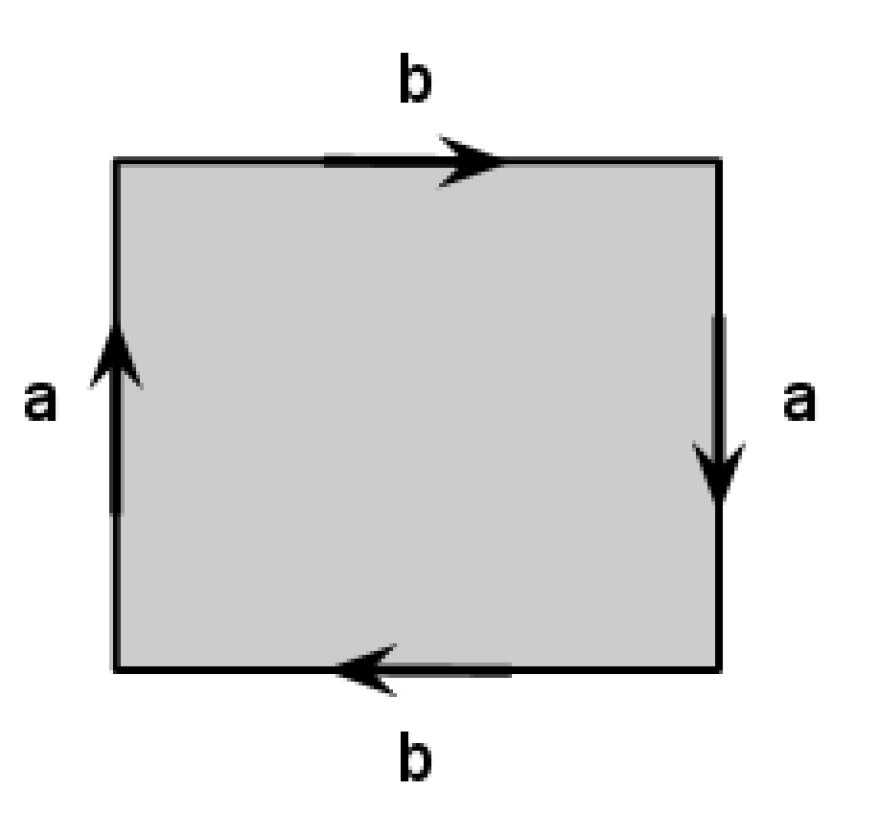
Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
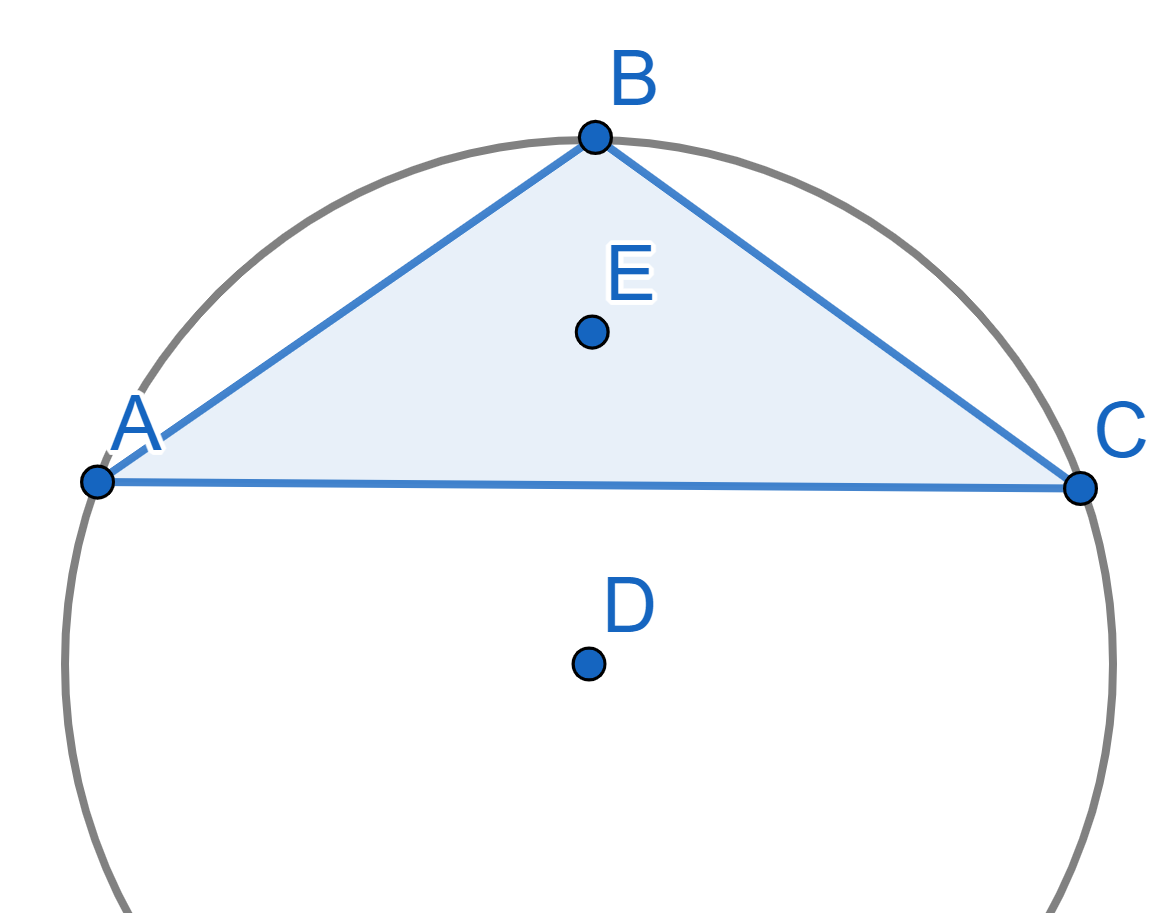
\(ABC\) is a triangle. The circumscribed circle is the circle that touches all three vertices of the triangle \(ABC\). It is also the smallest circle lying entirely outside the triangle. The center of the circumscribed circle is \(D\).
The inscribed circle is the circle which touches all three sides of the triangle \(ABC\). It is also the largest circle lying entirely inside the triangle. The center of the inscribed circle is \(E\).
The points \(D\) and \(E\) are symmetric with respect to the segment \(AC\). Find the angles of the triangle \(ABC\).
