Problems

Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.

Imagine the Earth is a perfectly round solid ball. Let us drill from the North Pole, London and Beijing simultaneously and meet at the centre of Earth. A ball with three openings is formed. The surface of this ball is shown on the left of the picture below. Describe how to stretch this surface so that it looks like the surface of a donut with two holes as shown on the right.

Prove that \(|x|\ge x\). It may be helpful to compare each of \(|3|\), \(|-4.3|\) and \(|0|\) with \(3\), \(-4.3\) and \(0\) respectively.

How many subsets of \(\{1, 2, . . . , n\}\) are there of even size?

In how many ways can \(\{1, . . . , n\}\) be written as the union of two sets? Here, for example, \(\{1, 2, 3, 4\}\cup\{4, 5\}\) and \(\{4, 5\}\cup\{1, 2, 3, 4\}\) count as the same way of writing \(\{1, 2, 3, 4, 5\}\) as a union.

Prove for any natural number \(n\) that \((n + 1)(n + 2). . .(2n)\) is divisible by \(2^n\).

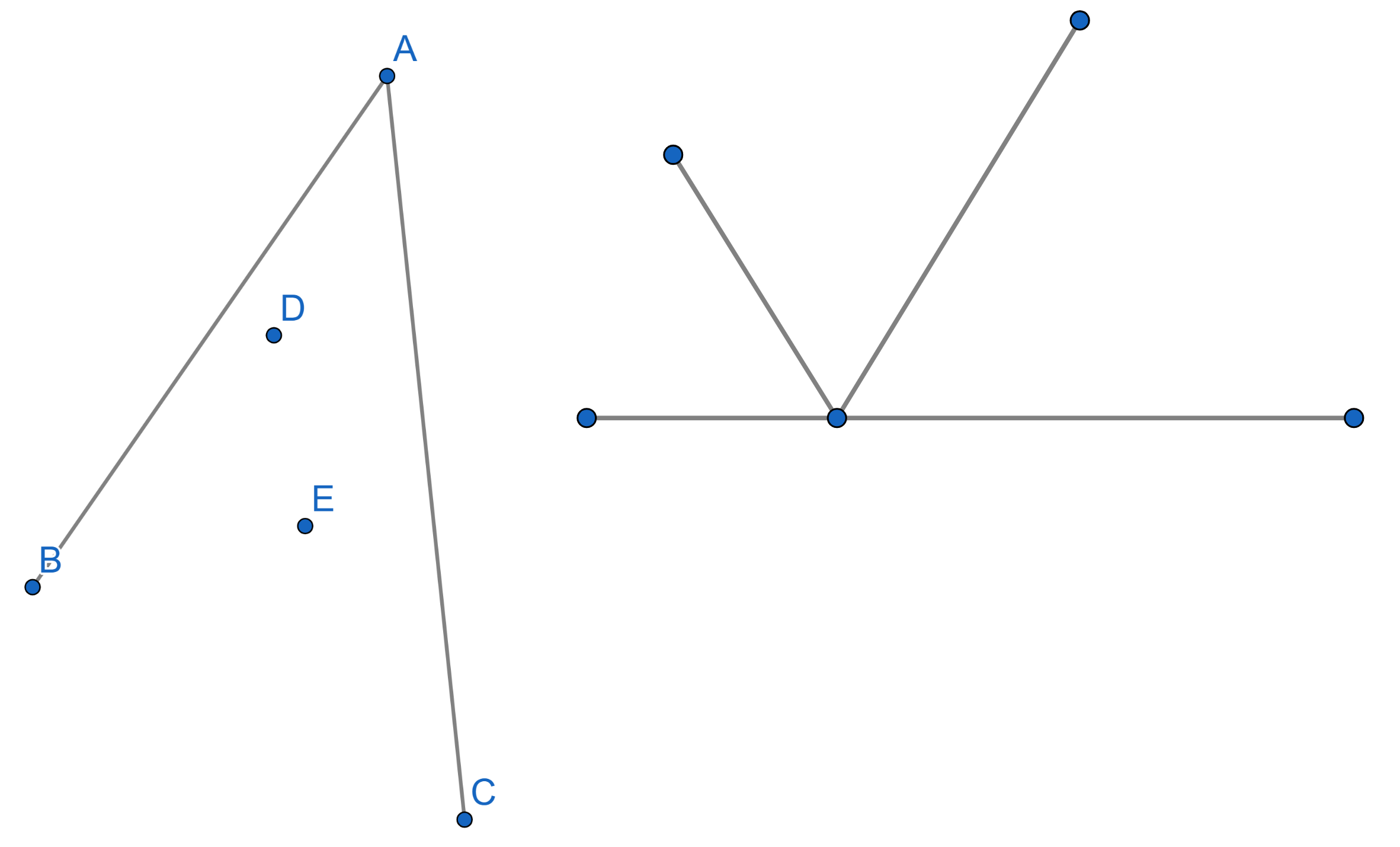
Between two mirrors \(AB\) and \(AC\), forming a sharp angle two points \(D\) and \(E\) are located. In what direction should one shine a ray of light from the point \(D\) in such a way that it would reflect off both mirrors and hit the point \(E\)?
If a ray of light comes towards a surface under a certain angle, it is reflected with the same angle as on the picture.

Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?

There is a triangle with side lengths \(a\), \(b\) and \(c\). Can you form a triangle with side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\) and \(c\) are? Give a proof if it is always possible or never possible. Otherwise, construct examples to show the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\) and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).

There is a triangle with side lengths \(a\), \(b\) and \(c\). Does there exist a triangle with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\) and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\) and \(z\) if and only if all the inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.