Problems
Prove that the product of five consecutive integers is divisible by \(120\).
Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.
Note: a graph is planar if it can be drawn in the plane with no edges
crossing. For example, three houses, each of which is connected to three
utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph
with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).
Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.
In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.
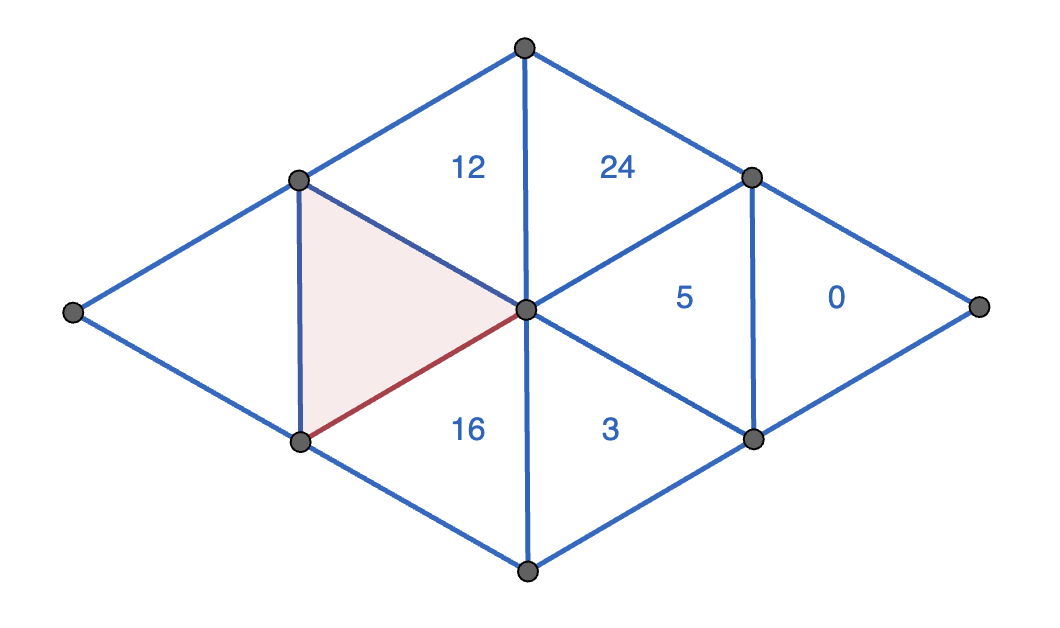
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.
How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive
digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have
\(8\) subsets overall but only \(5\) contain no consecutive integers. The
\(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three
of these.
Mary, who wrote an online computer game, plans to assign every user a
unique password.
a) Currently, she wants to have passwords that are \(8\) symbols long and are all made from
lowercase letters \(a,b,c\). How many
different passwords can she generate?
b) Her friend suggested a modification: use 8-symbol words made from
letters \(a,b,c\), with exactly one
capital letter, and also include one digit (\(0-9\)). How many times more passwords can
she generate now?
How many numbers in the set \(\{ 1,2,3, \dots, 1000 \}\) can be expressed as a sum of \(6\) consecutive integer numbers?
How many \(7\)-digit numbers, larger than \(6\) million, are there such that the product of their digits is \(42\)?
Here is a half of a magic trick to impress your friends. Take the Ace to Seven of hearts and order them numerically in a pile with Ace at the bottom and Seven at the top. Do the same with the Ace to Seven of spades. Put the pile of spades on top of the pile of hearts. Flip the \(14\)-card deck so the cards are now face down.
Make a cut anywhere. Deal out \(7\) cards from the top into a pile, so that you now have two piles of equal size again. Let us refer to the motion of taking the top card of a pile and putting it to the bottom as making a swap. Making two swaps means doing the motion twice, NOT taking the top two cards at the same time.
Your friend chooses two nonnegative numbers that add up to \(6\), for example \(4\) and \(2\). Make \(4\) swaps on the first pile and \(2\) swaps on the second pile. Remove the top card of each pile, so that we now have two piles of six cards.
Your friend now chooses two nonnegative numbers that add up to five and repeat the same procedure. We will continue doing this, but at each turn, the total number of swaps decreases by one. Eventually, we should have one card remaining in each pile. It turns out to be a matching pair.
How does the trick work?
Many magicians can perform what is known as the Faro shuffle. Actually there are two kinds of Faro shuffle: the in Faro shuffle and the out Faro shuffle.
Let us assume that the deck has an even number of cards. The first step of the Faro shuffle is to divide the deck into two smaller decks of equal size. One deck consist of the top half of the original deck in their original order. The other deck consists of the bottom half of the original deck in their original order.
The second step of the Faro shuffle is to interweave the two decks, so that each card is above and beneath a card of the opposite deck. This is where the in Faro and the out Faro differ: the in Faro changes the top and bottom cards of the original deck (from before step one) while the out Faro retains the original top and bottom cards.
Show that only 8 out Faro shuffles are needed to return a standard 52 card deck back into its original position.
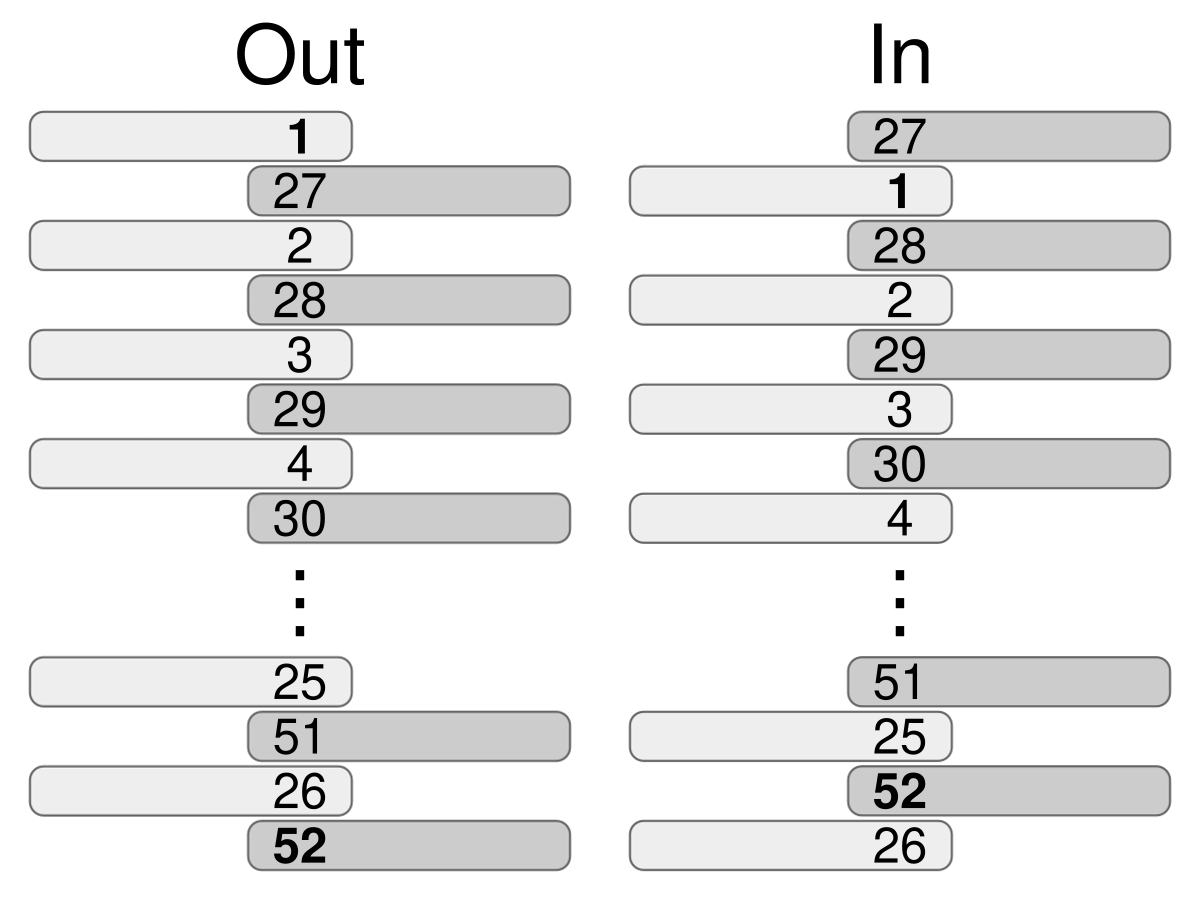
How can you move the top card to any position in an even size deck using only Faro shuffles?