Problems

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

How many integers are there \(n>1\) such that \(a^{25}-a\) is divisible by \(n\) for every integer \(a\).

Let \(p\) be a prime number, \(a\) be an integer, not divisible by \(p\). Prove that \(a^p-a\) is divisible by \(p\).

Let \(n\) be an integer. Denote by \(\phi(n)\) the number of integers from \(1\) to \(n-1\) coprime to \(n\). Find \(\phi(n)\) in the following cases:

• \(n\) is a prime number.

• \(n = p^k\) for a prime \(p\).

• \(n=pq\) for two different primes \(p\) and \(q\).

Let \(n\) be an integer and let \(a\) be an integer coprime to \(n\). Prove that \(a^{\phi(n)-1}-1\) is divisible by \(n\).

We have a square of side length 1. At each vertex of the square, we draw a circle of radius 1. What is the area bounded by all four circles?

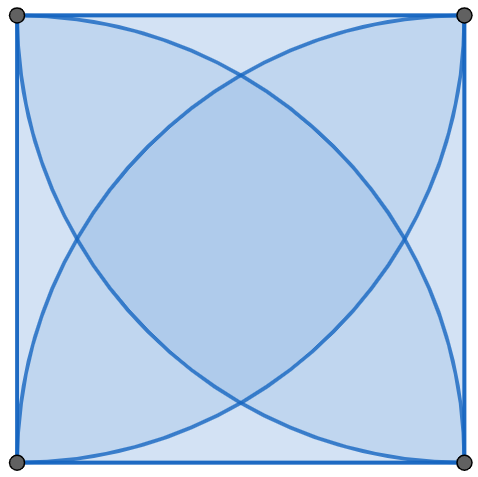
Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).

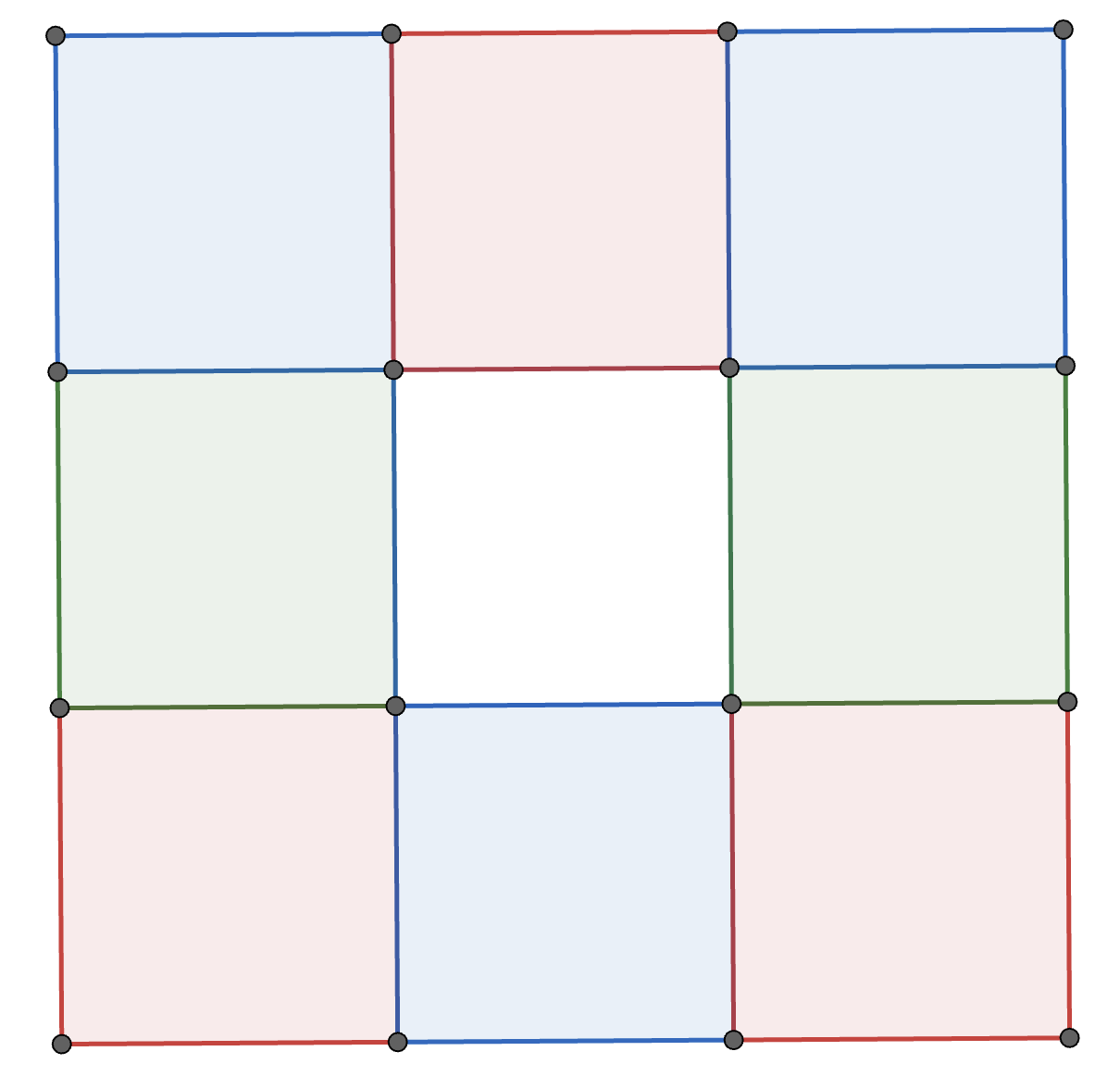
Each square in a \(3\times3\) grid of squares is coloured red, white, blue, or green so that every \(2\times2\) square contains one square of each color. One such colouring is shown below. How many different colourings are possible?

For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?