Problems

A bin has \(2\) white balls and \(3\) black balls. You play a game as follows: you draw balls one at a time without replacement. Every time you draw a white ball , you win a dollar, but every time you draw a black ball, you lose a dollar. You can stop the game at any time. Devise a strategy for playing this game which results in an expected profit.

Take a (finite) set \(S\), say \([n]\) and a random function \(f:S\to S\). What’s the distribution of the limiting size of the image of the iterates of \(f\)?

That is, \(\lim_{N\to\infty}|f^N([n])|\)

By random, let \(i\in[n]\). Each \(f(i)\) is independently and identically distributed as uniform random variables on \([n]\). One can also think of it as \(f\) is taken uniformly from the \(n^n\) possible functions \([n]\to[n]\).

In the picture below, there are the \(12\) pentominoes. Is it possible to tile a \(6\times10\) rectangle with them?

Show how to tile a \(5\times12\) rectangle with the twelve pentominoes.

Show how to tile a \(4\times15\) rectangle with the twelve pentominoes.

Is it possible to tile a \(3\times20\) rectangle with the twelve pentominoes?

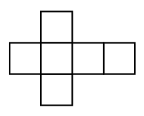
Show to how to cover the plane with this cube net:

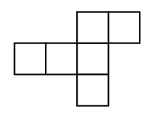
Show how to tile the plane with this cube net:

Queen Hattius has two prisoners and gives them a puzzle. If they succeed, then she’ll let them free. She will randomly put a hat on each of their heads. The hats could be red or blue. They will simultaneously guess the colour of their own hat, and if at least one person is correct, then they win.

Each prisoner can only see the other prisoner’s hat - and not their own. The prisoners aren’t allowed to communicate once they’re wearing the hats, but they’re allowed to come up with a strategy before.

What should their strategy be?

Two children come in from playing outside, and both of their faces are muddy. Their dad says that at least one of their faces is muddy. He’ll repeat this phrase until all of the children with muddy faces have come forward. Assuming that the children can’t see or feel their own face, but that they’re perfect at logic, what happens?