Problems
Let \(s>2\) and \(t>2\) be integers. Show that \(R(s,t)\le R(s-1,t)+R(s,t-1)\).
The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?
Find, with proof, all integer solutions of \(a^3+b^3=9\).
Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\), namely a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=0}^{n}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\] Where next to \(a_i\) there is a point with coordinate where \(1\) is in \(i\)-th place. The point \((0,0,...,0)\) belongs to the simplex as well.
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Consider a simplicial subdivision given by pairwise connected middles of
all the segments in the original simplex. Assign the numbers \(0,1,2...,n\) to the subdivision vertices in
such a way as to conduct a Sperner’s coloring in such a way that you
will have only one rainbow simplex.
(USO 1974) Let \(a,b,c\) be three distinct integers, and let \(P(x)\) be a polynomial whose coefficients are all integers. Prove that it is not possible that the following three conditions hold at the same time: \(P(a)=b, P(b)=c,\) and \(P(c)=a\).
For a polynomial \(P(x)=ax^2+bx+c\), consider the following two kinds of transformations:
Swap coefficients \(a\) and \(c\). Hence the polynomial \(P(x)\) becomes \(cx^2+bx+a\) after this transformation.
For any number \(t\) of your choice, change the variable \(x\) into \(x+t\). For example, with the choice of \(t=1\), after this transformation, the polynomial \(x^2+x+1\) becomes \((x+1)^2+(x+1)+1=x^2+3x+3\).
Is it possible, using only a sequence of these two transformations, to change the polynomial \(x^2-x-2\) into the polynomial \(x^2-x-1\)?
Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?
On a \(5\times5\) “Lights Out” board, it turns out that there is a simple rule to turn the whole board off regardless of which lights are on at the start:
Chase down. Start at the top row. For each light in that row that is turned on, press the button directly below it so that it turns off. Move to the next row and repeat. This turns off rows one by one; only the bottom row may be left with lights being on.
Fix the bottom. Find your bottom row in the table and press on the top row the pattern shown to the right. Then chase down again. Repeat until everything is off.
| Lights on bottom row | Press on top row | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| # | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| 1 | ON | OFF | OFF | OFF | ON | ON | ON | OFF | OFF | OFF |
| 2 | OFF | ON | ON | OFF | OFF | ON | OFF | ON | OFF | OFF |
| 3 | OFF | OFF | ON | ON | OFF | OFF | OFF | ON | ON | OFF |
| 4 | ON | OFF | ON | ON | OFF | OFF | ON | OFF | ON | OFF |
Can you explain why this works?
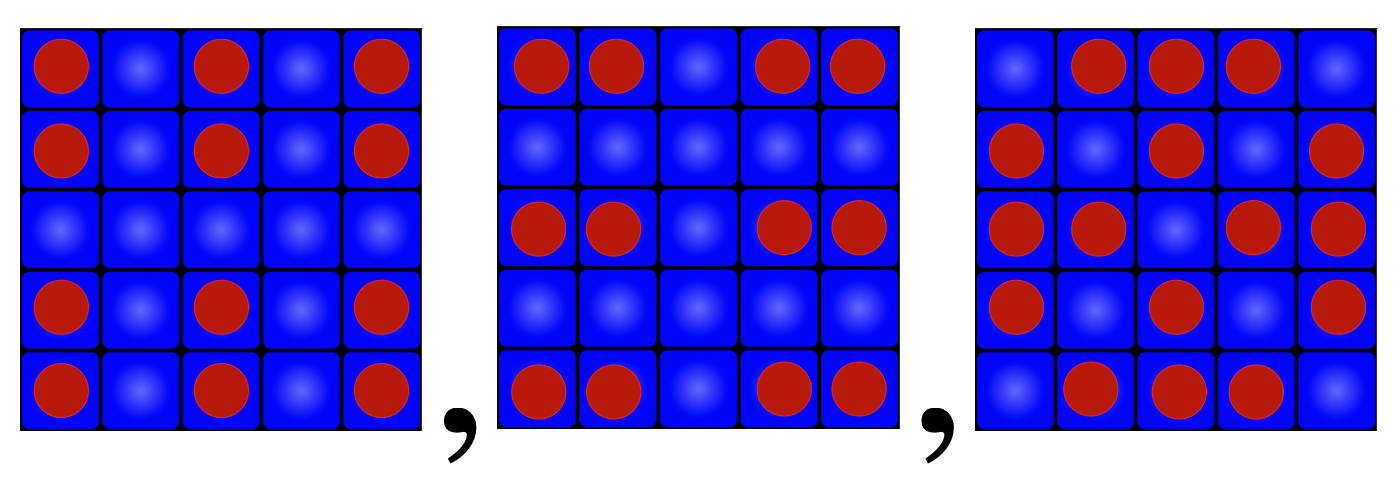
George is playing on the \(5\times 5\) “Lights Out" board and says that since each light can be on or off, and there are \(25\) lights on the board, the number possible light patterns that can be achieved by playing the game is \(2^{25}\). It turns out that the number is much smaller, it is \(2^{23}\). Can you explain why? You may take it as a fact that these three are the only quiet plans of the \(5\times 5\) board:
Let \(n\) be any whole number. Show that the product \((n+1)(n+2)\cdots(2n)\) is divisible by \(2^n\).