Problems
In the middle of the Dark Forest in Wonderland there is a large square clearing, where a wolf is sitting right is the middle of the square, and four dogs are sitting at the four vertices of the square. The wolf can run inside the square with maximum speed \(v\), while the dogs can run along the edges of the square with the speed \(1.5v\). It is known that the wolf kills a dog if they meet one to one, and two dogs kill the wolf if they overpower it together. Can the wolf escape from that square into the forest?
You have two sticks and matchbox. Each stick takes exactly an hour to burn from one end to the other. The sticks are not identical and do not burn at a constant rate. As a result, two equal lengths of the stick would not necessarily burn in the same amount of time. How would you measure exactly 45 minutes by burning these sticks?
One of your employees insists on being paid daily in gold. You have a gold bar whose value is that of seven days’ salary for this employee. The bar is already segmented into seven equal pieces. If you are allowed to make just two cuts in the bar, and must settle with the employee at the end of each day, how do you do it?
You have a 3-quart bucket, a 5-quart bucket, and an infinite supply of water. How can you measure out exactly 4 quarts?
Suppose you had eight billiard balls, the recruiter began. One of them is slightly heavier, but the only way to tell is by put-ting it on a scale against the others. What’s the fewest number of times you’d have to use the scale to find the heavier ball?
How many times a day do a clock’s hands overlap?
How do you cut a rectangular cake into two equal pieces when someone has already removed a rectangular piece from it? The removed piece can be of any size or orientation. You are allowed just one straight cut.
Why does a mirror reverse right and left instead of up and down?
After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:
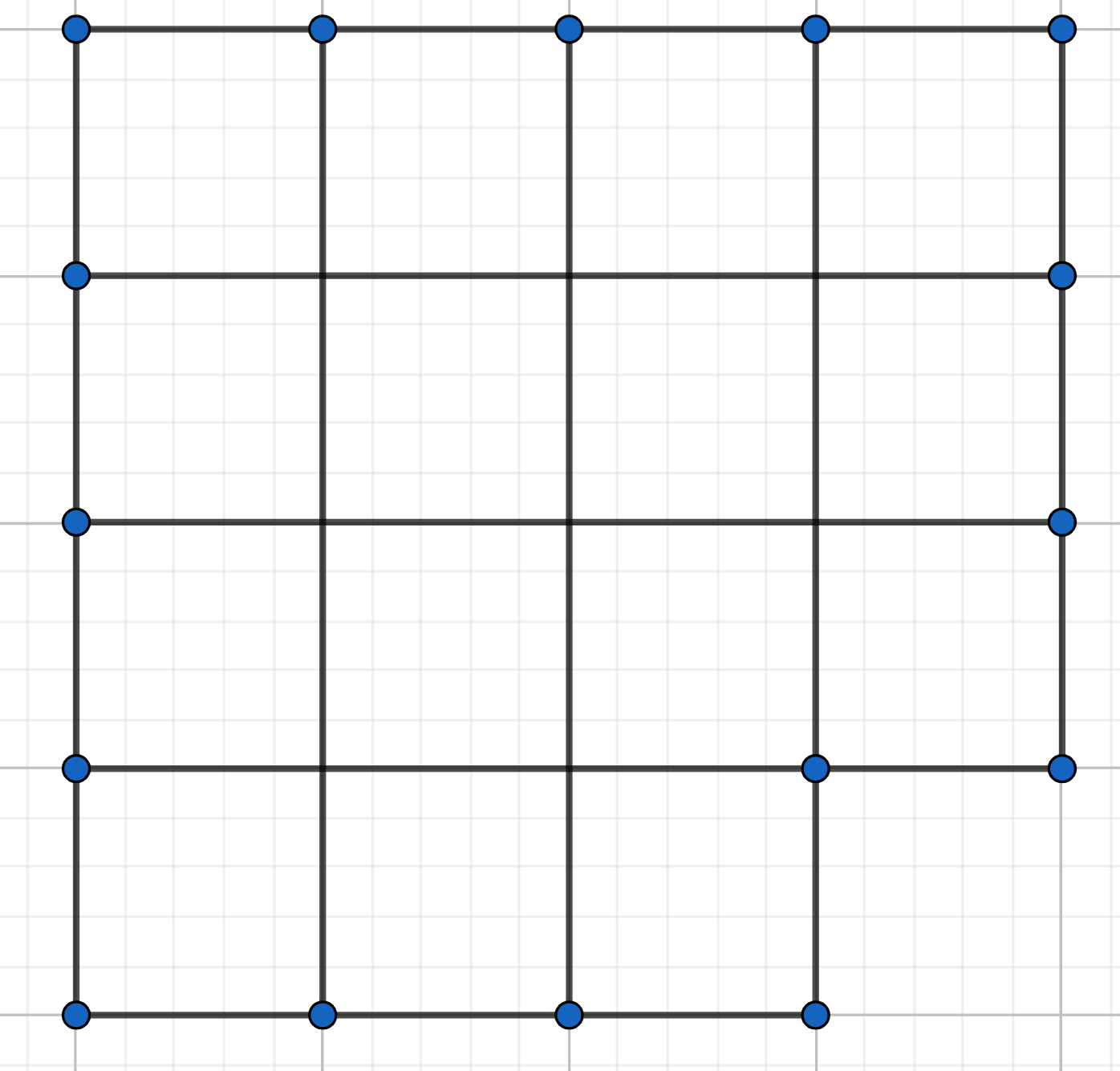
how can we cut this into three congruent shapes?
Max asked Emily how old she was. She replied that she was 13 years old the day before yesterday, and will be 16 next year. Then, Max asked her brother, whether it was true, and he said yes. How is it possible if nobody was lying?