Problems
In the jungle, \(100\) monkey families live on tree houses, which we think of the little squares arranged on a \(10\times 10\) square grid. Today it turns out that \(9\) of these houses have been infected with Bananavid-19, which spreads every day! Thankfully, a healthy home can only be infected if has at least two infected neighbours (we don’t count diagonals on the grid as neighbours), prove that the infection will not spread to the whole monkey village.
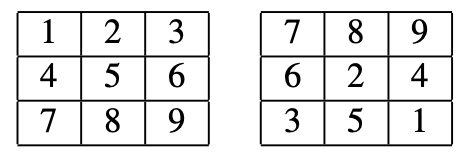
Consider the two following grids. We consider two of the little squares to be a neighbor if they share a side (so that diagonals don’t count as neighbours). You are allowed to choose any two neighbouring little squares and add the same whole number to both squares. Show that by repeating this step, you cannot turn the first grid into the second one.
We build a sequence of numbers as follows: the first six terms are \(1,0,1,0,1,0\) and from then onwards, the next term of the sequence is equal to the last digit of the sum of the last \(6\) terms of the sequence. For example: if we had at some point the numbers \(1,0,3,5,10,9\) the next term would be the last digit of \(1+0+3+5+10+9=28\), i.e: \(8\). Will the terms \(0,1,0,1,0,1\) ever appear in the sequence?
On a board there are the following \(+\) and \(-\) signs drawn:
\[+\; + \; + \; - \; - \; + \; + \; - \; + \; - \; +\]
You can choose any two signs, erase them, and then draw a \(+\) sign if the signs you erased were both equal, and a \(-\) sign if the signs you erased were different. Show that regardless of the order you perform these erasures, the sign that is left at the end is always the same.
\(2025\) lilly pads are placed in a row. Some number of frogs are on top of the pads. Each minute, if there are two frogs on the same lily pad, and this lily pad is not at one of the ends of the row, some two of the frogs will jump: one to the left lily pad, and one to the right lily pad (they will jump in opposite directions) show that this process cannot repeat forever.
Darya has made eleven pancakes, each has an area of \(1\), but each pancake can have a different shape. She places them carefully on a plate of area \(6\). Show that if the pancakes fit entirely inside the plate, then there must be two pancakes that overlap by at least an area of \(1/11\).
Prove that there is no oscillator of period \(4\) (i.e: the whole pattern repeats every \(4\) generations) which has exactly one cell that also has period \(4\).
A pattern \(P\) is called a garden of Eden if there exists no pattern \(P'\) distinct to \(P\) such that \(P'\) evolves into \(P\) after one generation. Show that a garden of Eden exists. You do not need to provide an example of such a pattern.
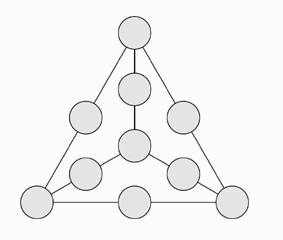
We would like to place the numbers \(1\) to \(10\) into the circles in the picture below, using each number exactly once, so that for every straight line of three circles, the numbers in those circles add up to the same total. Is this possible?
We have a \(17\) digit number, and we form a new number by reading the original number from right to left (if this produces a leading zero, we simply ignore this leading zero, giving a \(16\) digit number). We add this new number to the original number. Show that this resulting sum will have at least one even digit.