Problems

There are \(2026\) people at a big party. Some pairs of people are friends (nobody is friends with themselves, and friendship goes both ways). Starting one minute after midnight, the host begins sending people home in a strange way.

After 1 minute, anyone with no friends at the party leaves. After 2 minutes, anyone with exactly one friend currently in the party leaves. After 3 minutes, anyone with exactly two friends currently in the party leaves, and so on.

(Important: at each minute, everyone checks their number of friends at the same time, and then all the people who qualify leave together.)

Show that after \(2026\) minutes have passed, at least two people will have left the party.

Let \(ABCD\) be a quadrilateral whose diagonals intersect at a point \(E\).

Consider the four triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\). For each triangle, draw its medians, and let \(K\), \(J\), \(M\), and \(L\) be the points where the medians intersect in the triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\), respectively.

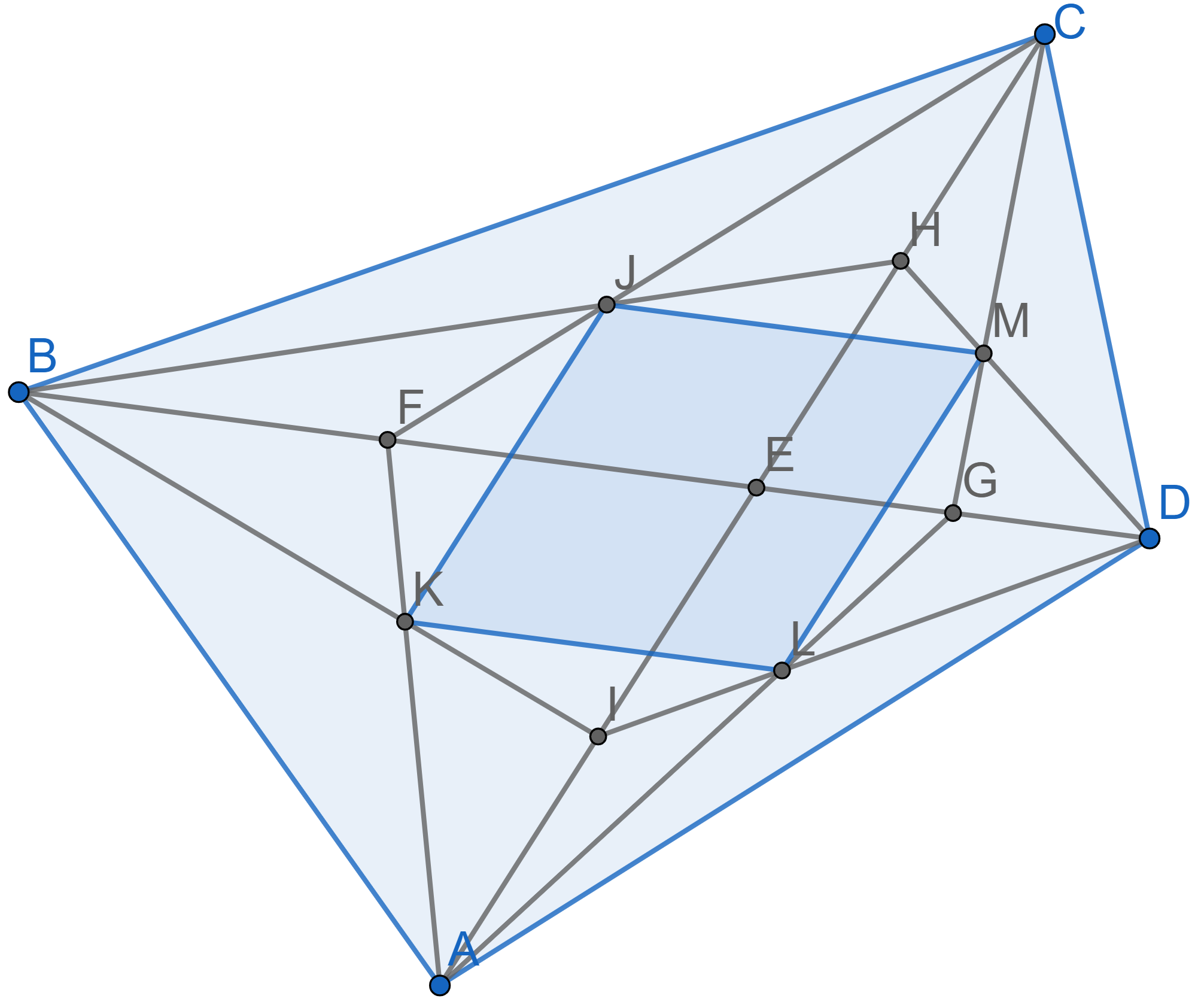
Prove that the quadrilateral \(KJML\) is a parallelogram.

You may wish to use the fact that the point of intersection of the medians of any triangle divides each median in the ratio \(2:1\), counting from the vertex, but if you use this fact, you should prove it.

For a trapezium \(ABCD\), let \(E\) be the point of intersection of the sides \(AB\) and \(CD\), and let the point \(G\) be the point of intersection of the diagonals of the trapezium. Finally, let \(F\) amd \(H\) be the midpoints of the sides \(BC\) and \(AD\) respectively.

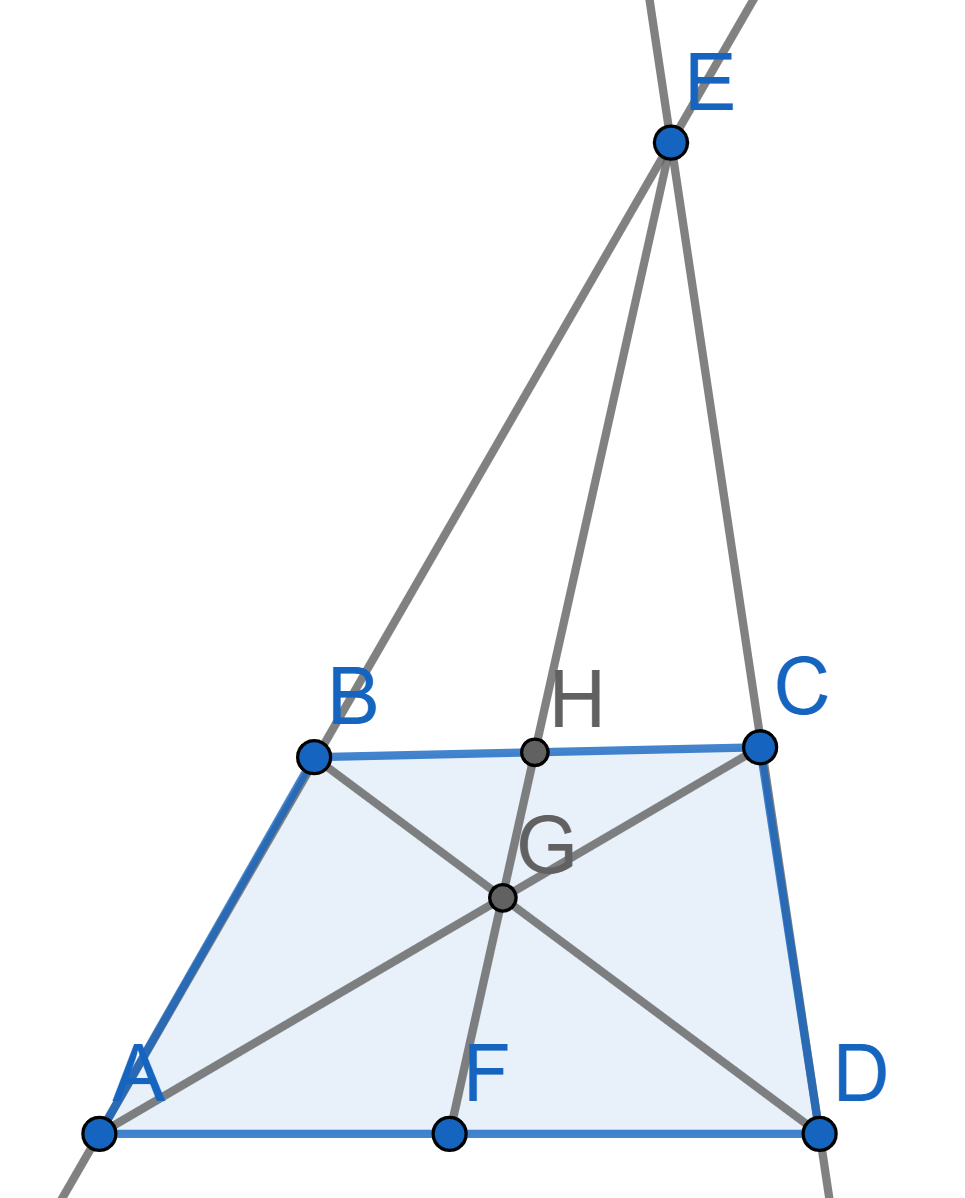
Prove that the points \(E,F,G,H\) lie on one line.

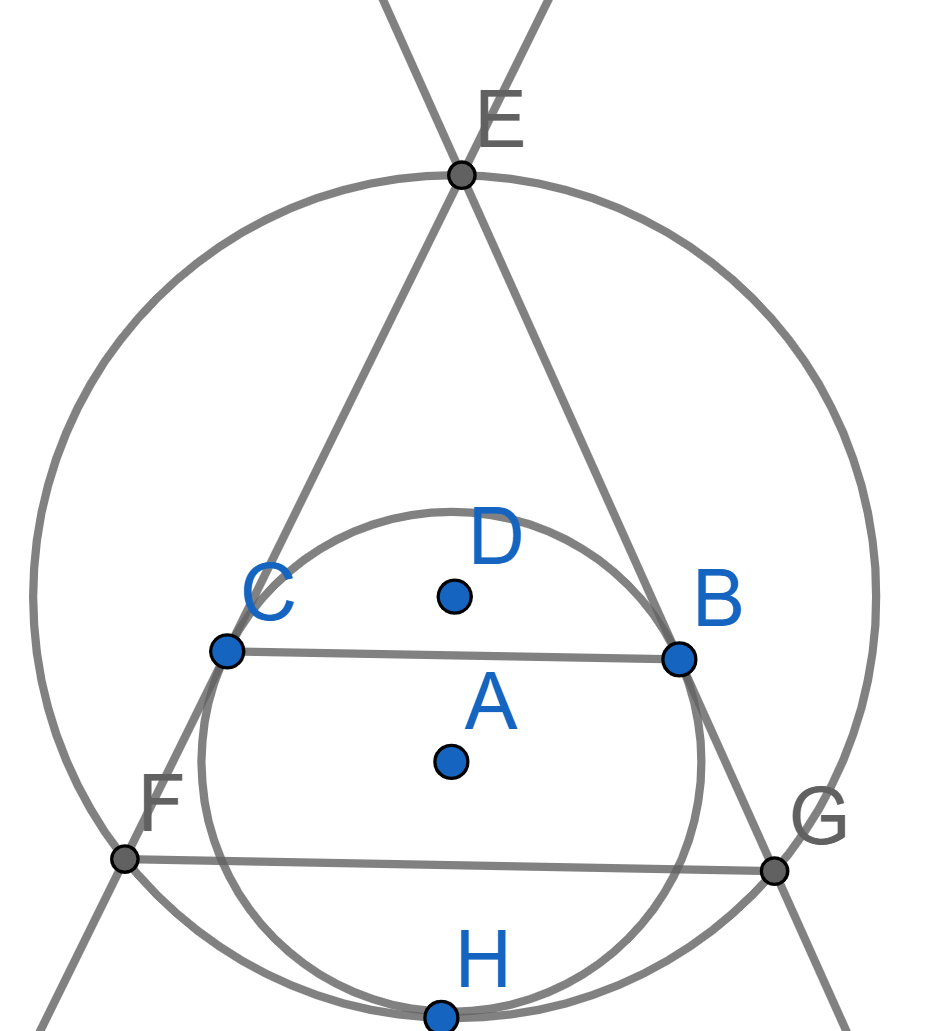
The triangle \(EFG\) is isosceles with \(EF=EG\). A circle with center \(A\) is tangent to the sides \(EF\) and \(EG\) at the points \(C\) and \(B\) respectively. It is also tangent to the circle circumscribed around the triangle \(EFG\) at the point \(H\). Prove that the midpoint of the segment \(BC\) is the center of the circle inscribed into the triangle \(EFG\).

Seven vertices of a cube are labelled with the number \(0\), and the remaining vertex is labelled with \(1\). You are allowed to repeat the following move: choose an edge of the cube and increase by \(1\) the numbers at both ends of that edge.

Is it possible to reach eight numbers that are all divisible by three?

Each number on the number line (not only whole numbers!) is painted black \((B)\) or white \((W)\). Is it always possible, regardless of how the number line is painted, to find a line segment such that both its endpoints and its middle point are painted with the same colour?

On the first day Robinson Crusoe tied the goat with a single piece of rope by putting one peg into the ground. What shape did the goat graze?