Problems

Pinoccio keeps his Golden Key in the safe that is locked with a numerical password. For secure storage of the Key he replaced some digits in the password by letters (in such a way that different letters substitute different digits). After replacement Pinoccio got the password \(QUANTISED17\). Honest John found out that:
• the number \(QUANTISED\) is divisible by all integers less than 17, and
• the difference \(QUA-NTI\) is divisible by \(7\).
Could he find the password?

Decipher the quote from Philip Pullmans "His Dark Materials":
Erh csy wlepp orsa xli xvyxl, erh xli xvyxl wlepp qeoi csy jvii.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Cut the "biscuit" into 16 congruent pieces. The sections are not necessarily rectilinear.

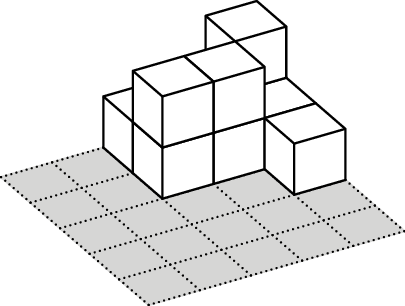
In the middle of an empty pool there is a square platform of \(50 \times 50\) cm, split into cells of \(10\times 10\) cm. Sunny builds towers of \(10\times 10\times 10\)cm cubes on the platform cells. After that his friend Margo turns on the water and counts how many towers are still above the water level. They call each visible tower an island.

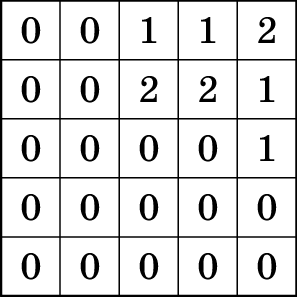
For example, let’s consider the case when the heights of the towers are as given in the table on the right. Then at the water level of \(5\) cm there is \(1\) island, at the water level of \(15\) cm there are two islands (if the islands have a common corner or don’t intersect at all, they are considered separate islands), and at the water level of \(25\) cm, all the towers are covered with water and there are \(0\) islands.

Find out how Sunny should build his towers to get the following numbers of islands corresponding to the level of water in the pool: \[\begin{array}{@{}*{26}{c}@{}} \textit{Water level (cm)}& 5& 15& 25& 35& 45\\ \textit{Number of islands}& 2& 5& 2& 5& 0 \end{array}\]

In the solution, write down how many cubes are there composing a tower in each cell as it is done in the example.

The king possesses \(7\) bags of gold coins, each containing \(100\) coins. While the coins in each bag appear identical, they vary in weight and they cannot be told apart by looking. The king recalls that within these bags, one contains coins that weigh \(7\)g each, another has coins weighing \(8\)g, the third bag contains coins weighing \(9\)g, the fourth has coins weighing \(10\)g, the fifth contains coins weighing \(11\)g, the sixth holds coins weighing \(12\)g, and finally, the seventh bag contains coins weighing \(13\)g each. However, he cannot remember which bag corresponds to which coin weight.
The king reported his situation to his chancellor, pointing to one of the bags, and asked how to determine the weight of the coins in that bag. The chancellor has large two-cup scales without weights. These scales can precisely indicate whether the weights on the cups are equal or, if not, which cup is heavier. Can the chancellor ascertain which coins are in the bag indicated by the king, using no more than two weightings? The chancellor is permitted to take as many coins as necessary to conduct the weightings.

Abigail’s little brother Carson found a big rectangular cake in the fridge and cut a small rectangular piece out of it.

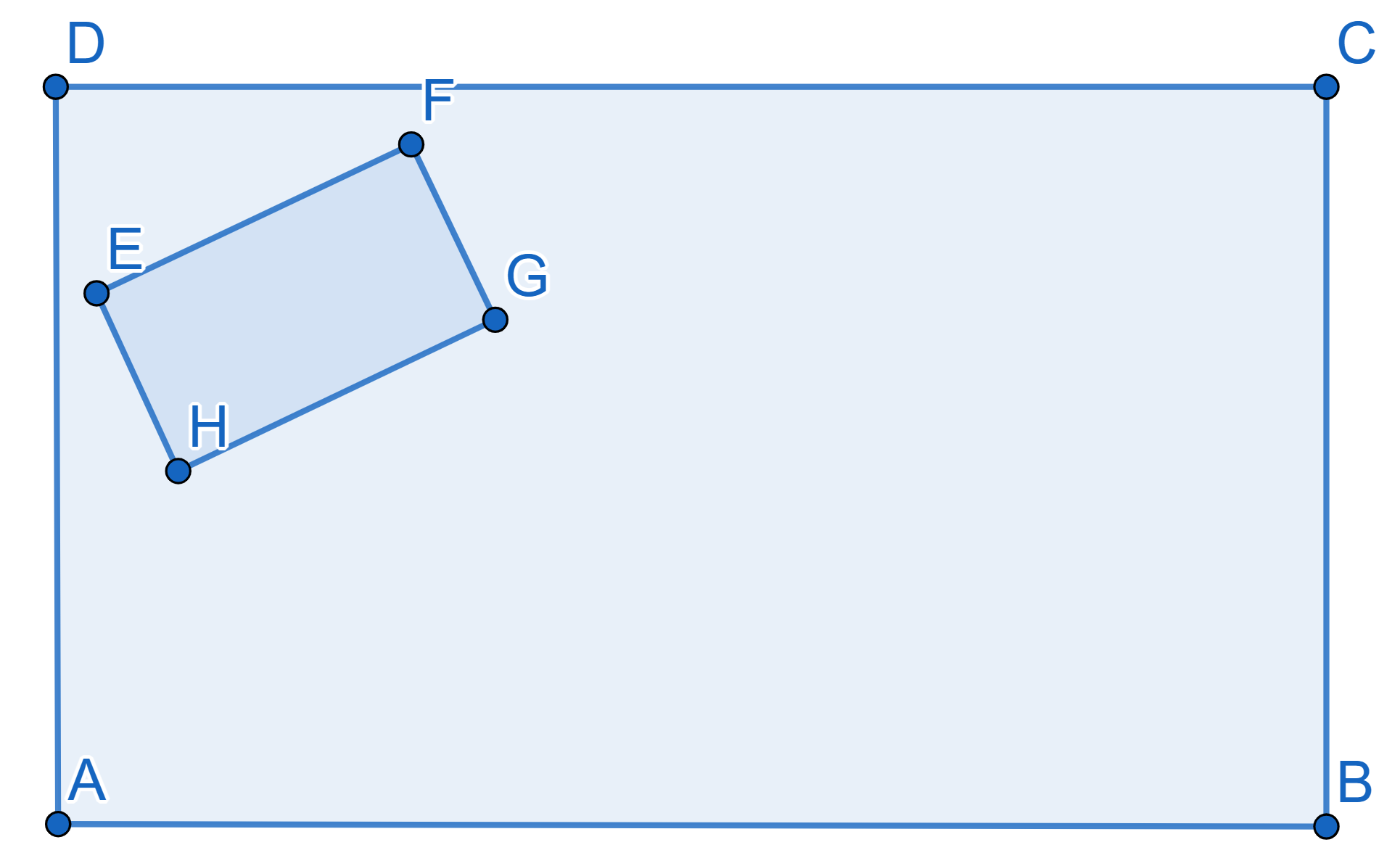
Now Abigail needs to find a way to cut the remaining cake into two pieces of equal area with only one straight cut. How could she do that? The removed piece can be of any size or orientation.

A chord of a circle is a straight line between two points on the circumference of the circle. Is it possible to draw five chords on a circle in such a way that there is a pentagon and two quadrilaterals among the parts into which these chords divide the circle?

There are \(20\) chairs in the room, which come in two colors: blue and red. Each chair is occupied by either a knight or a liar. Knights always tell the truth, while liars always lie. Initially, each of those seated claimed to be sitting on a blue chair. Then, they switched seats, after which half of the participants asserted that they were now sitting on blue chairs, while the other half claimed to be sitting on red ones. How many knights are currently occupying red chairs?

All the positive fractions smaller than \(1\) with denominators not more than \(100\) are written in a row. Isley and Ella put signs \("+"\) or \("-"\) in front of any fraction, which does not yet have a sign before it. They write signs in turns, but it is known that Isley has to make the last move and calculate the resulting sum. If the total sum turns out to be an integer number, then Ella will give her a chocolate bar. Will Isley be able to get a chocolate bar regardless of Ella’s actions?

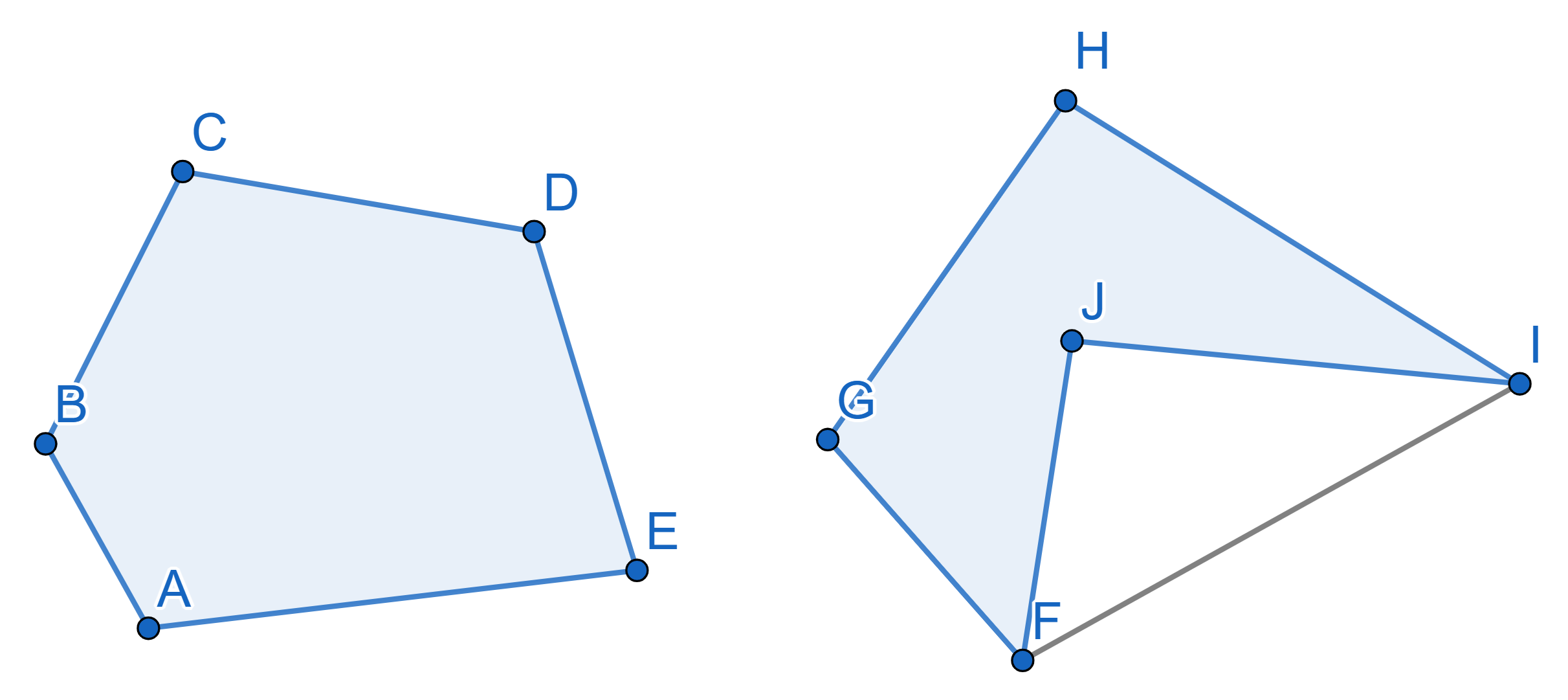
We say that a figure is convex if a segment connecting any two points lays fully within the figure. On the picture below the pentagon on the left is convex and the one on the right is not.

Is it possible to draw \(18\) points inside a convex pentagon so that each of the ten triangles formed by its sides and diagonals contains equal amount of points?