Problems

This is a famous problem, called Monty Hall problem after a popular TV show in America.
In the problem, you are on a game show, being asked to choose between three doors. Behind each door, there is either a car or a goat. You choose a door. The host, Monty Hall, picks one of the other doors, which he knows has a goat behind it, and opens it, showing you the goat. (You know, by the rules of the game, that Monty will always reveal a goat.) Monty then asks whether you would like to switch your choice of door to the other remaining door. Assuming you prefer having a car more than having a goat, do you choose to switch or not to switch?

Each integer on the number line is coloured either yellow or blue. Prove that there is a colour with the following property: For every natural number \(k\), there are infinitely many numbers of this colour divisible by \(k\).

There are \(100\) non-zero numbers written in a circle. Between every two adjacent numbers, their product was written, and the previous numbers were erased. It turned out that the number of positive numbers after the operation coincides with the amount of positive numbers before. What is the minimum number of positive numbers that could have been written initially?

Definition A set is a collection of elements, containing only one copy of each element. The elements are not ordered, nor they are governed by any rule. We consider an empty set as a set too.
There is a set \(C\) consisting of \(n\) elements. How many sets can be constructed using the elements of \(C\)?

There are six letters in the alphabet of the Bim-Bam tribe. A word is any sequence of six letters that has at least two identical letters. How many words are there in the language of the Bim-Bam tribe?

Consider a set of numbers \(\{1,2,3,4,...n\}\) for natural \(n\). Find the number of permutations of this set, namely the number of possible sequences \((a_1,a_2,...a_n)\) where \(a_i\) are different numbers from \(1\) to \(n\).

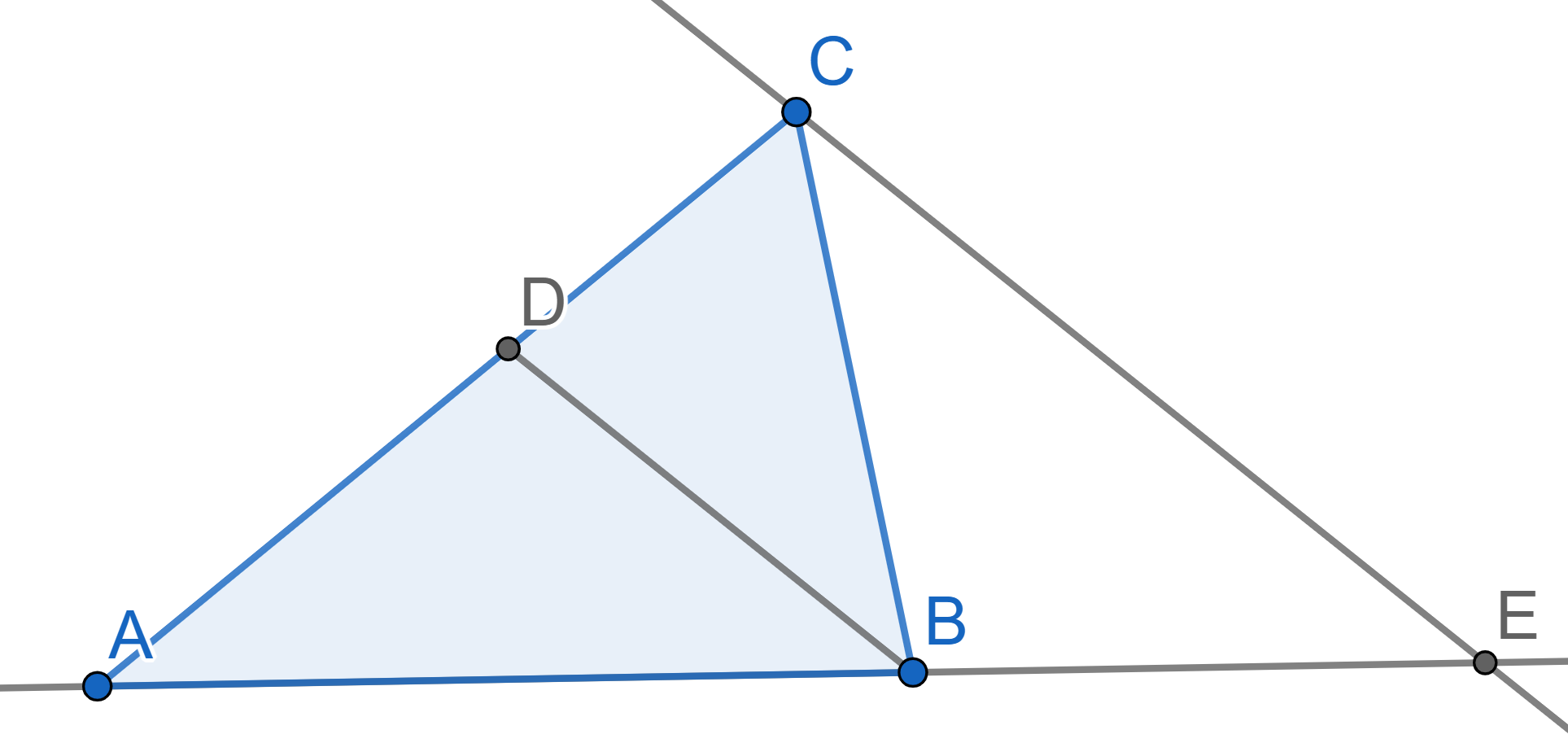
On the diagram below the line \(BD\) is the bisector of the angle \(\angle ABC\) in the triangle \(ABC\). A line through the vertex \(C\) parallel to the line \(BD\) intersects the continuation of the side \(AB\) at the point \(E\). Find the angles of the triangle \(BCE\) triangle if \(\angle ABC = 110^{\circ}\).

We want to wrap \(12\) Christmas presents in different coloured paper. We have \(6\) different patterns of paper and we want to use each one exactly twice. In how many ways can we do this?

Mr Roberts wants to place his little stone sculptures of vegetables on the different shelves around the house. He has \(17\) sculptures in total and three shelves that can fit \(7\), \(8\) and \(2\) sculptures respectively. In how many ways can he do this?
The order of sculptures on the shelf does not matter.

In a certain state, there are three types of citizens:

• A fool considers everyone a fool and themselves smart;

• A modest clever person knows truth about everyone’s intellectual abilities and consider themselves a fool;

• A confident clever person knows about everyone intellectual abilities correctly and consider themselves smart.

There are \(200\) deputies in the High Government. The Prime Minister conducted an anonymous survey of High Government members, asking how many smart people are there in the High Government. After reading everyone’s response he could not find out the number of smart people. But then the only member who did not participate in the survey returned from the trip. They filled out a questionnaire about the entire Government including themselves and after reading it the Prime Minister understood everything. How many smart could there be in the High Government (including the traveller)?