Problems

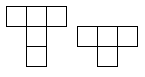
Draw a shape that can be cut into \(4\) copies of the figure on the left or into \(5\) copies of the figure on the right (the figures can be rotated).

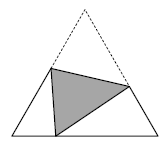
A equilateral triangle made of paper bends in a straight line so that one of the vertices falls on the opposite side as shown on the picture. Show that the corresponding angles of the two white triangles are equal.

There are \(100\) people in a room. Each person knows at least \(67\) others. Show that there is a group of four people in this room that all know each other. We assume that if person \(A\) knows person \(B\) then person \(B\) also knows person \(A\).

The numbers \(a\) and \(b\) are integers and the number \(p \ge 3\) is prime. Suppose that \(a+b\) and \(a^2 +b^2\) are divisible by \(p\). Show that \(a^2 + b^2\) is divisible by \(p^2\).

There are \(33\) cities in the Republic of Farfarawayland. The delegation of senators wants to pick a new capital city. They want this city to be connected by roads to every other city in the Republic. They know for a fact that given any set of \(16\) cities, there will always be some city that is connected by roads to all those selected cities. Show that there exists a suitable candidate for the capital.

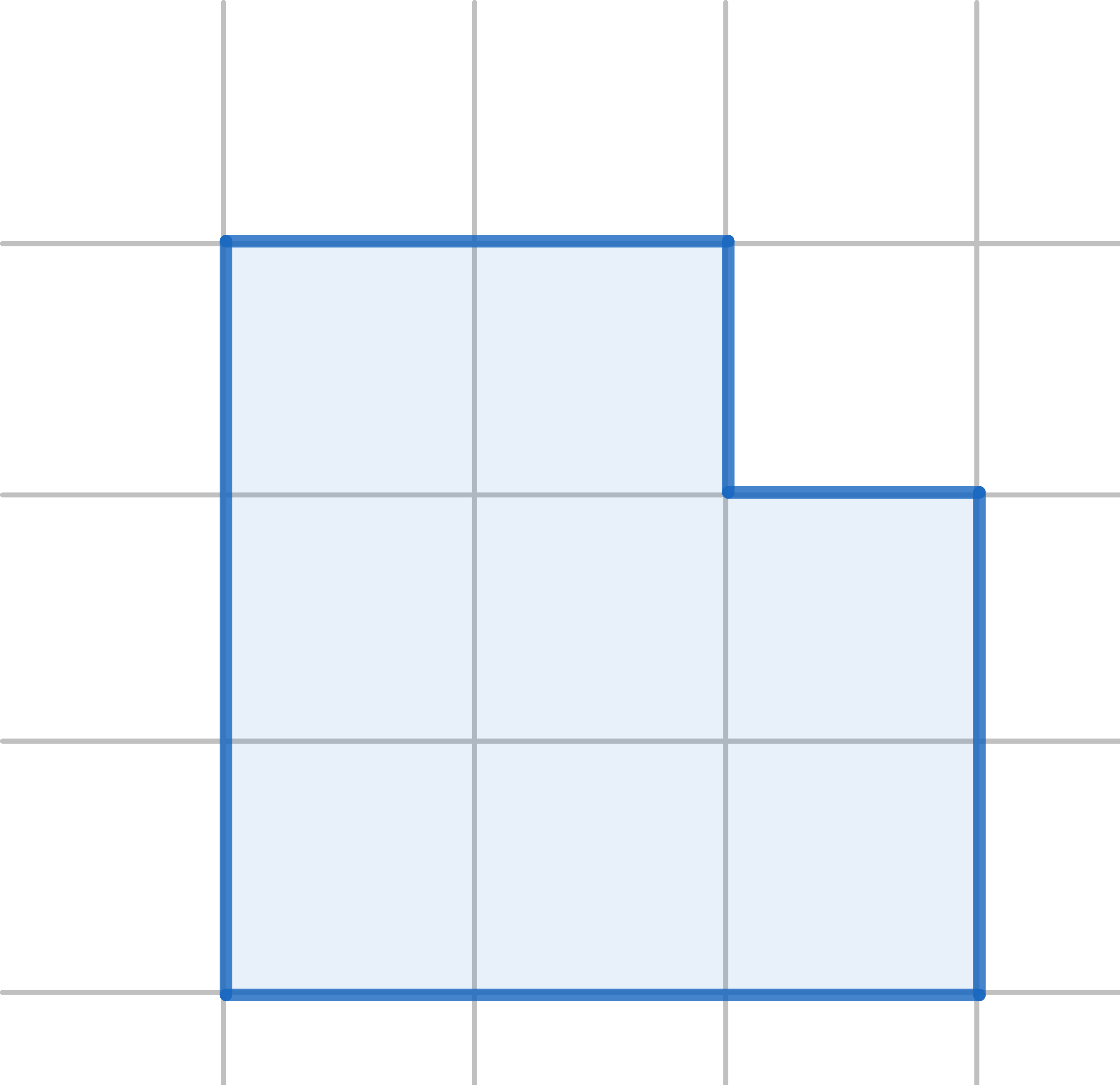
The diagram shows a \(3 \times 3\) square with one corner removed. Cut it into three pieces, not necessarily identical, which can be reassembled to make a square:

Find all possible non-zero digits \(A\) for which the following holds \((AA+AA+1) \times A = AAA\). (Recall \(AA\) means the two-digit number whose first and second digits are \(A\))

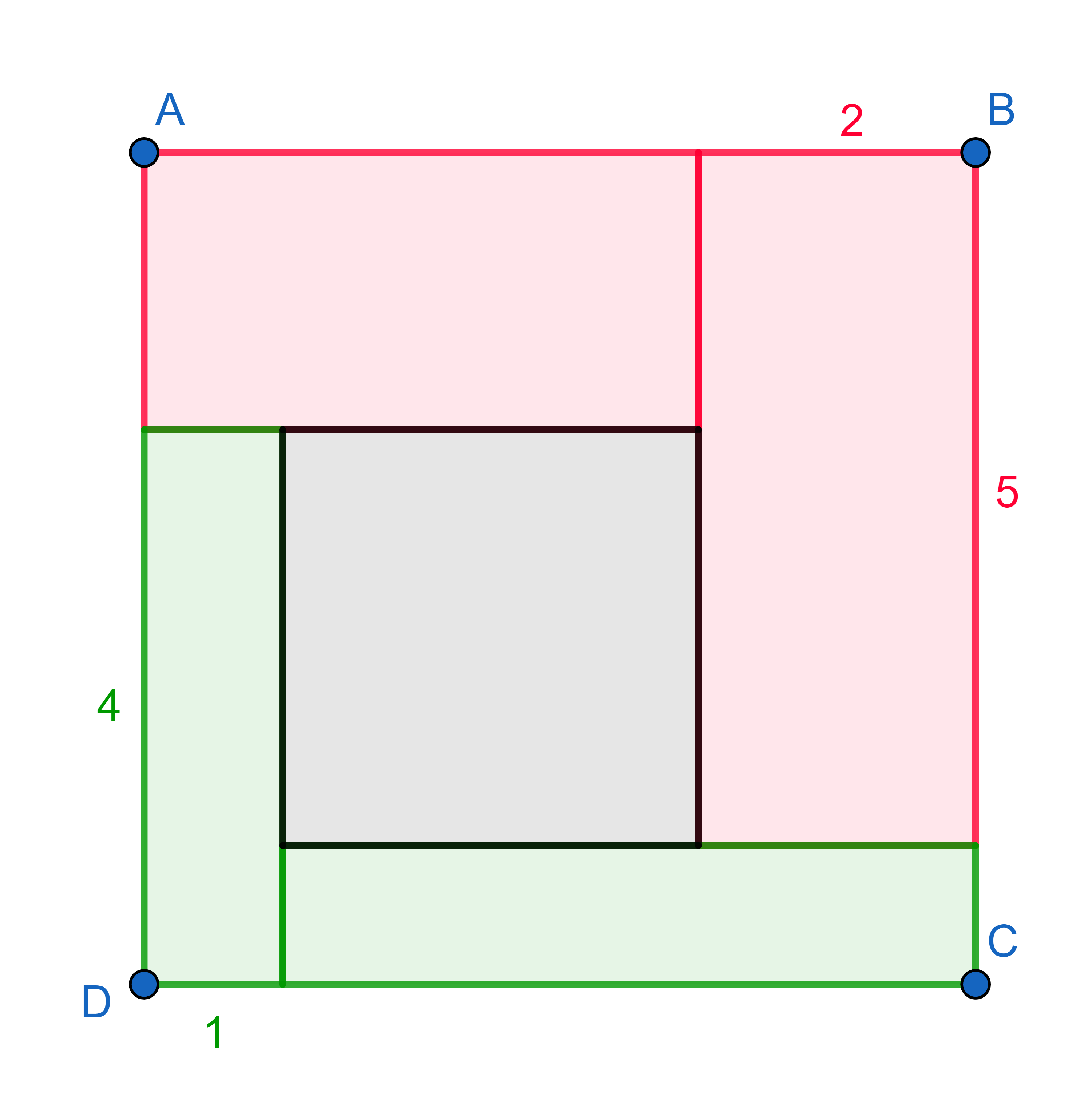
A square has been divided into \(4\) rectangles and a square. If the rectangle in the bottom left corner has dimensions \(1 \times 4\) and the one in the top right is \(2 \times 5\), what is the area of the small square in the middle?

There are \(25\) bugs sitting on the squares of a \(5 \times 5\) board, \(1\) at each square. When I clap my hands, each bug jumps to a square diagonally from where it was before. Show that after I clap my hands, at least \(5\) squares will be empty.

In a convex quadrilateral \(ABCD\), all the triangles \(\triangle ABC\), \(\triangle BCD\), \(\triangle CDA\) and \(\triangle DAB\) have equal perimeters. Show that \(ABCD\) is a rectangle.