Problems
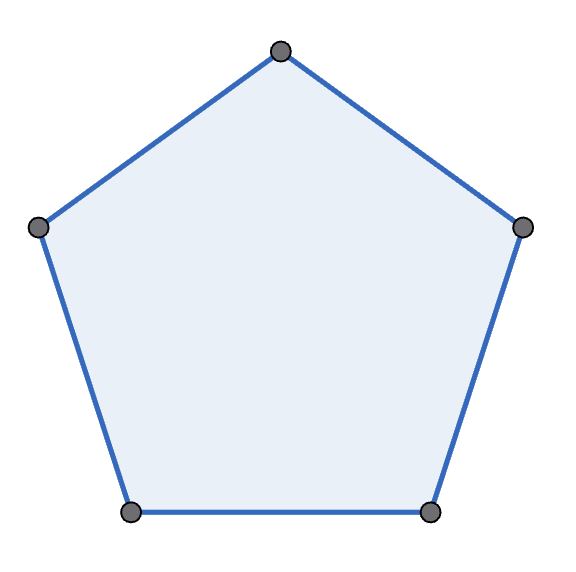
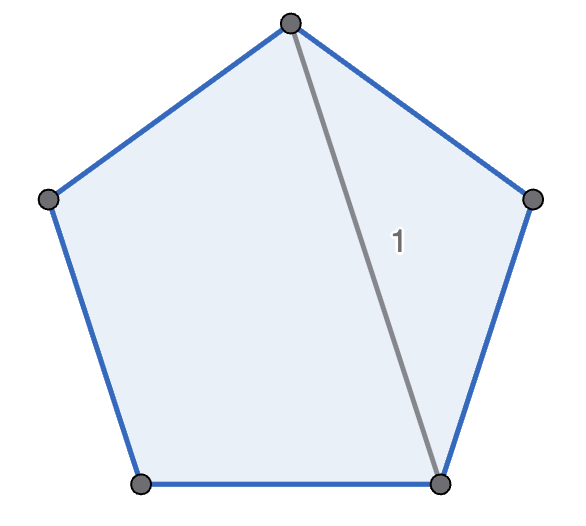
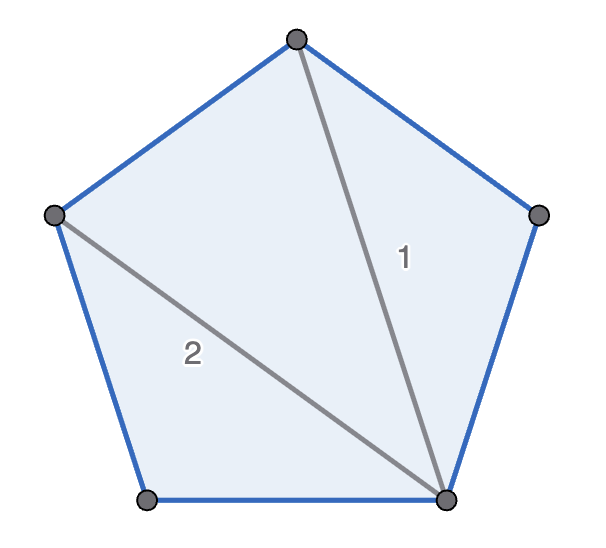
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).
Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).
Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.
Using \(R(s,t)\le R(s-1,t)+R(s,t-1)\), prove that \(R(k,k)\le 4^k\).
Prove the general version of Sperner’s lemma: Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\). Strictly speaking a simplex is a convex linear combination of \(n+1\) points in general position (when \(k\) points are never in one subspace of dimension \(k-1\)). One can view it as an \(n\)-dimensional tetrahedron or a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=1}^{n+1}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\]
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Prove that every Sperner’s coloring of any subdivision of an \(n\)-dimensional simplex contains an odd
number of rainbow simplexes, namely whose vertices are colored using all
\(n+1\) colors.
Prove that the only solution to \(5^a-3^b=2\) with \(a,b\) being positive integers is \(a=b=1\).
Show that Pell’s equation \(x^2-dy^2=1\) has a nontrivial solution.
Without using any wolves, show that Robinson’s goat can only graze shapes that are convex (that means, whenever you pick two points inside the shape, the whole line between them also lies inside). But if Robinson is allowed to use as many wolves as he likes, this restriction disappears. Show that in this case, he can make the goat graze in the shape of any polygon at all.
In a field, there are two pegs, \(A\) and \(B\), placed \(15\) metres apart. Each peg has a small
ring on top, and a rope can slide freely through these rings.
You have one rope and two goats that want to graze the grass, but they
will fight each other if they can both reach the same spot.
The rope may be arranged in any way you choose: it could pass through
both rings, only one, or neither, depending on your setup.
For what lengths of rope can you arrange things so that the goats cannot
fight each other?