Problems

Show that the difference between two consecutive square numbers is always odd.

Find the contrapositive of the statement: “If in every school there is a class with at least \(20\) students, then there is a school with at least \(10\) students".

Show that given any three numbers, at least two of them will have the same parity. Recall that the parity of a number is whether it is odd or even.

Show that given any \(6\) whole numbers - not necessarily consecutive - at least two of them will have the same remainder when divided by \(5\).

Show that given any \(3\) numbers, there will be two of them so that their difference is an even number.

Show that if \(k\) is a positive whole number, then the decimal expansion of \(1/k\) either has a finite number of decimal places or eventually repeats. For example, \[\frac{1}{5} = 0.2 \qquad\text{or}\qquad \frac{1}{17} = 0.\underbrace{0588235294117647}_{} \underbrace{0588235294117647}_{}\ldots\]

George is cutting a birthday cake into various numbers of pieces. If he cuts the cake or a piece of cake into only two parts, then those part must have equal weight. However, if he cuts the cake into more than two pieces, then those pieces can be of any weight, but they all must have different integer masses. After some operations he managed to cut the cake into \(N\) pieces. Is it true that for any \(N\geq 10\) it could be that all the pieces are of the same weight?

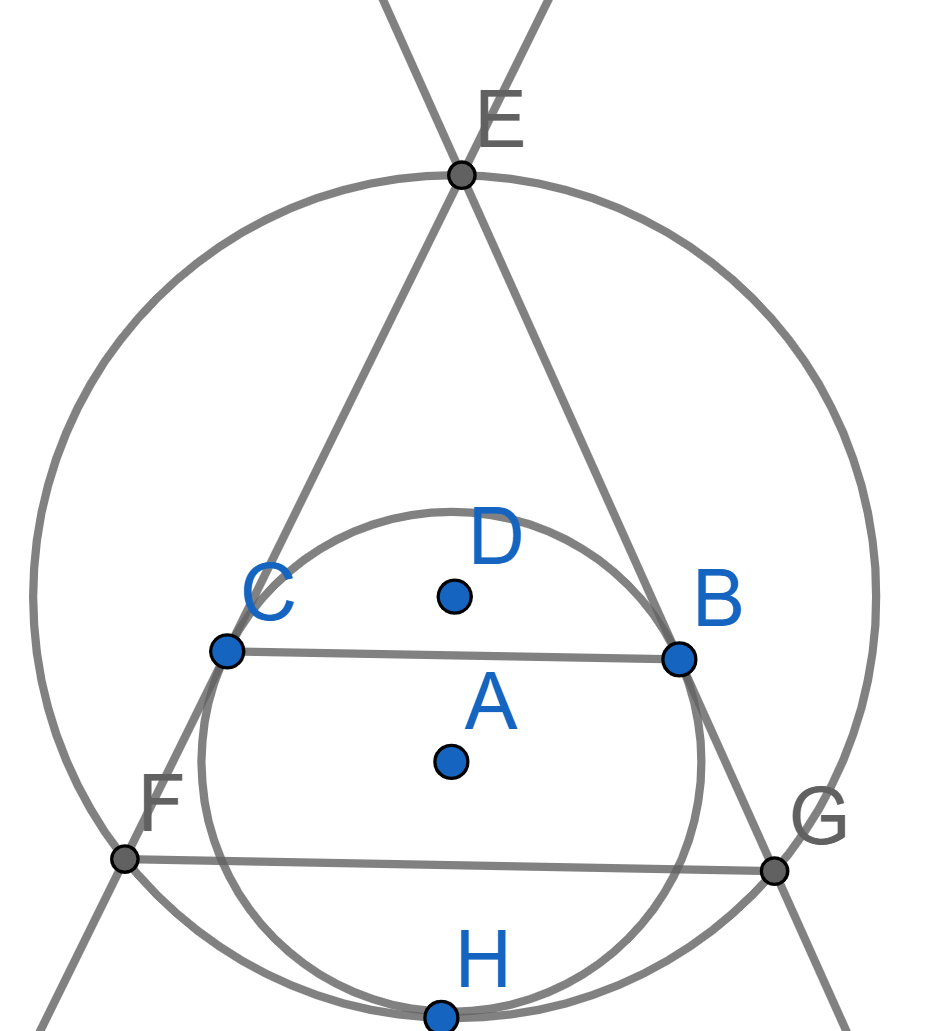
The triangle \(EFG\) is isosceles with \(EF=EG\). A circle with center \(A\) is tangent to the sides \(EF\) and \(EG\) at the points \(C\) and \(B\) respectively. It is also tangent to the circle circumscribed around the triangle \(EFG\) at the point \(H\). Prove that the midpoint of the segment \(BC\) is the center of the circle inscribed into the triangle \(EFG\).

For a triangle \(ABC\) denote by \(R\) the radius of the circle superscribed around \(ABC\), by \(r\) the radius of circle inscribed into \(ABC\). Prove that \(R\geq 2r\) and equality holds if and only if the triangle \(ABC\) is regular. For this problem, you may want to search about the “Euler Circle” online.

On the first day Robinson Crusoe tied the goat with a single piece of rope by putting one peg into the ground. What shape did the goat graze?