Problems

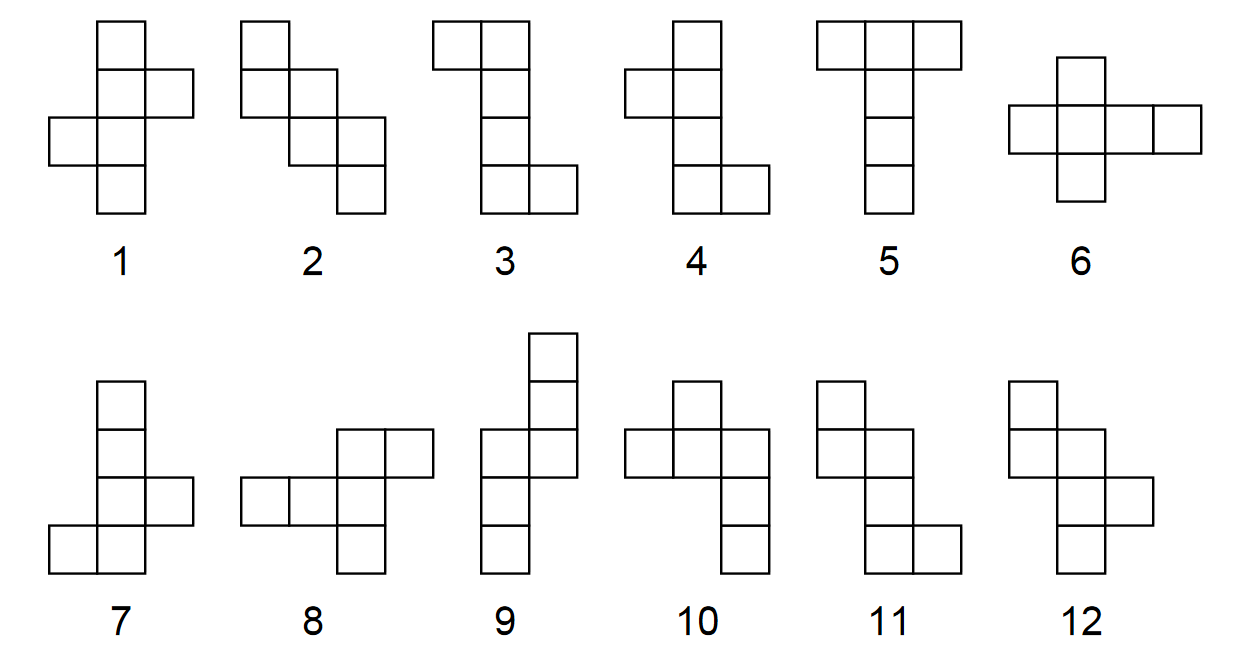
David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

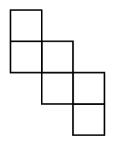
It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:

Can two tied wolves keep an untied goat in a triangle?

While studying numbers and their properties, Robinson came across a three-digit prime number whose last digit equals the sum of the first two digits. What are the options for the last digit of this number, given that none of its digits is zero?

When Robinson Crusoe and his friend Friday learned about divisibility rules, Friday decided to proposed his own rule:

if a number is divisible by \(27\), then the sum of its digits is also divisible by \(27\).

Was Friday right?

One day Friday multiplied all the numbers from 1 to 100. The product appeared to be a pretty large number, and he added all the digits of that number to receive a new smaller number. Even then he did not think the number was small enough, and added all the digits again to receive a new number. He continued this process of adding all the digits of the newly obtained number again and again, until finally he received a one-digit number. Can you tell what number was it?

Robinson Crusoe’s friend Friday was looking at \(3\)-digit numbers with the same first and third digits. He soon noticed that such number is divisible by \(7\) if the sum of the second and the third digits is divisible by \(7\). Prove that he was right.

2016 digits are written in a circle. It is known, that if you make a number reading the digits clockwise, starting from some particular place, then the resulting 2016-digit number is divisible by 27. Show that if you start from some other place, and moving clockwise make up another 2016-digit number, then this new number is also divisible by 27.

Louise is confident that all her classmates have different number of friends. Is she right?

There are 100 cities all connected by roads. Each city has 6 roads coming in (or going out). How many roads do connect those cities?