We solve problems

Problem #PRU-35771

Problems Functions of one variable. Continuity Periodicity and aperiodicity Methods Examples and counterexamples. Constructive proofs Calculus

15–16 4.0

Does a continuous function that takes every real value exactly 3 times exist?

Problem #PRU-57006

Problems Geometry Plane geometry Quadrilateral Circumscribed quadrilaterals

13–16 4.0

Prove that a convex quadrilateral \(ICEF\) can have a circle inscribed into it if and only if \(IC+EH = CE+IF\).

Problem #PRU-57808

Problems Geometry Plane geometry Plane transformations Parallel translation

13–15 4.0

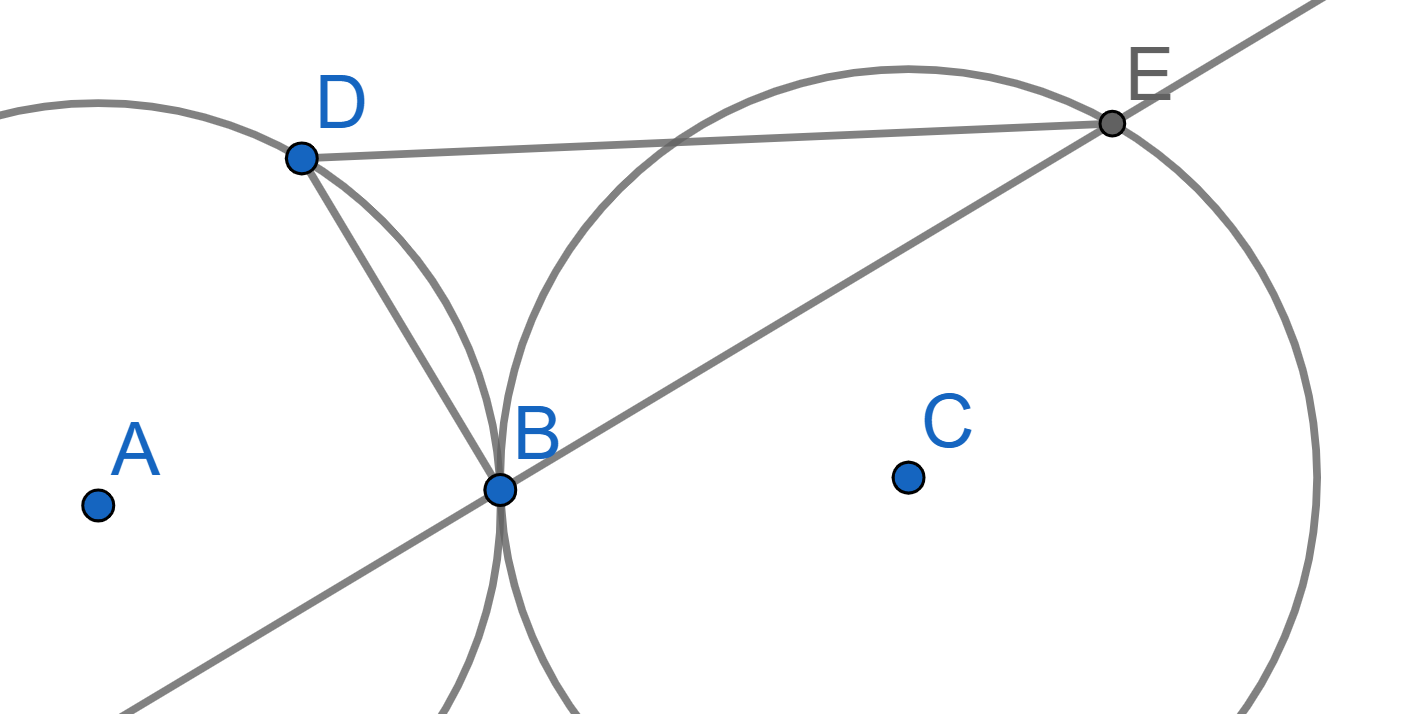
Two circles of radius \(R\) touch at point \(B\). On one of them, point \(D\) is chosen and on the other point \(E\) is chosen. These points have a property of \(\angle DBE = 90^{\circ}\). Prove that \(DE = 2R\).

Problem #PRU-58082

Problems Geometry Plane geometry Geometrical inequalities Inequalities in a triangle A segment inside the triangle is smaller than the largest side ,Problems Geometry Plane geometry Triangles Types of triangles Right-angled triangles Pythagorean theorem and its converse

12–14 4.0

A \(3\times 4\) rectangle contains 6 points. Prove that amongst them there will be two points, such that the distance between them is no greater than \(\sqrt5\).

Problem #PRU-58084

Problems Geometry Plane geometry Methods Circles Pigeonhole principle (angles and lengths) Pigeonhole principle (finite number of poits, lines etc.) Circle, sector, segment, etc Pigeonhole principle

12–13 4.0

There are 25 points on a plane, and among any three of them there can be found two points with a distance between them of less than 1. Prove that there is a circle of radius 1 containing at least 13 of these points.

Problem #PRU-58085

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Covers Geometry Plane geometry Polygons Inscribed and circumscribed polygons Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

13–15 4.0

A unit square contains 51 points. Prove that it is always possible to cover three of them with a circle of radius \(\frac{1}{7}\).

Problem #PRU-58089

Problems Geometry Plane geometry Methods Pigeonhole principle (finite number of poits, lines etc.) Convex and non-convex figures Convex polygons Pigeonhole principle

12–15 4.0

What is the minimum number of points necessary to mark inside a convex \(n\)-gon, so that at least one marked point always lies inside any triangle whose vertices are the vertices of the polygon?

Problem #PRU-58094

Problems Geometry Plane geometry Methods Circles Pigeonhole principle (angles and lengths) Connection between the arc length, the angle, and the chord Central angle. Arc length and circumference Pigeonhole principle

13–15 4.0

Several chords are drawn through a unit circle. Prove that if each diameter intersects with no more than \(k\) chords, then the total length of all the chords is less than \(\pi k\).

Problem #PRU-58101

Problems Geometry Plane geometry Area Quadrilateral Area of a circle, sector, segment Parallelogram Special cases Rectangles and squares. Criteria and properties

14–15 4.0

A square of side 15 contains 20 non-overlapping unit squares. Prove that it is possible to place a circle of radius 1 inside the large square, so that it does not overlap with any of the unit squares.

Problem #PRU-60299

Problems Methods Divisibility Divisibility of a number. General properties Algebraic methods Partitions into pairs and groups; bijections Number Theory Pigeonhole principle Pigeonhole principle (other)

13–15 4.0

From the set of numbers 1 to \(2n\), \(n + 1\) numbers are chosen. Prove that among the chosen numbers there are two, one of which is divisible by another.