Problems

In the centre of a rectangular billiard table that is 3 m long and 1 m wide, there is a billiard ball. It is hit by a cue in a random direction. After the impact the ball stops passing exactly 2 m. Find the expected number of reflections from the sides of the table.

The mathematics teacher suggested changing the voting scheme at the performance competition. Currently, two groups compete in the final. In the first group, there are \(n\) pupils from class 5A, and in the second, there are \(n\) pupils from class 5B. \(2n\) mothers of all \(2n\) students attended the final of the competition. The best performance is chosen by the mothers voting. It is known that exactly half of the mothers vote honestly for the best performance, and the other half, in any case, vote for the performance in which her child participates (see problem number 65299). The teacher believes that it is necessary to choose a jury of \(2m\) people \((2m \ensuremath{\leq} n)\) from all \(2n\) mums at random. Find the probability that the best performance will win under such voting conditions.

A numerical set \(x_1, \dots , x_n\) is given. Consider the function \(d(t) = \frac{min_{i=1,\dots ,n}|x_i-t| + max_{i=1,\dots ,n}|x_i - t|}{2}\).

a) Is it true that the function \(d (t)\) takes the smallest value at a single point, for any set of numbers \(x_1, \dots , x_n\)?

b) Compare the values of \(d (c)\) and \(d (m)\) where \(c = \frac{min_{i=1,\dots ,n}x_i + max_{i=1,\dots ,n}x_i}{2}\) and \(m\) is the median of the specified set.

James furiously cuts a rectangular sheet of paper with scissors. Every second he cuts a random piece by an unsystematic rectilinear cut into two parts.

a) Find the mathematical expectation of the number of sides of a polygon (made from a piece of paper) that James randomly picks up after an hour of such work.

b) Solve the same problem if at first the piece of paper had the form of an arbitrary polygon.

In the Valley of the Five Lakes there are five identical lakes, some of which are connected by streams (in the image, dotted lines denote the possible “routes” of streams). Small carps are born only in lake \(S\). While the carp is growing up, it passes exactly four times from one lake to another by some stream (the carp chooses a stream at random), and then it remains in the lake in which it ended up. Of every thousand carps, an average of 375 remain in lake \(S\), and the rest remain in lake \(B\), no one else lives in the other lakes. Determine how many streams there are in the Valley of the Five Lakes.

A regular dice is thrown many times. Find the mathematical expectation of the number of rolls made before the moment when the sum of all rolled points reaches 2010 (that is, it became no less than 2010).

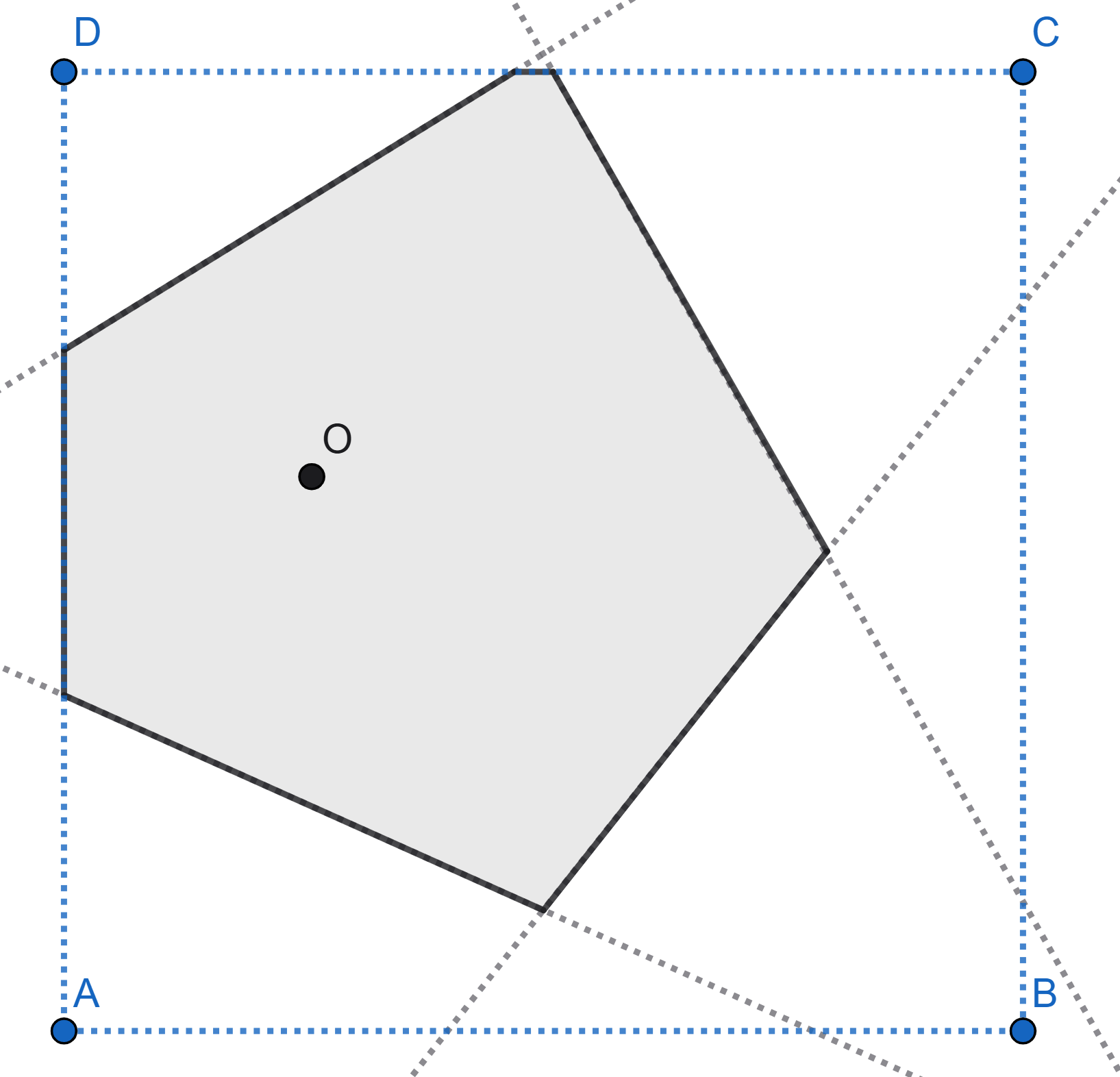
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.

The bus has \(n\) seats, and all of the tickets are sold to \(n\) passengers. The first to enter the bus is the Scattered Scientist and, without looking at his ticket, takes a random available seat. Following this, the passengers enter one by one. If the new passenger sees that his place is free, he takes his place. If the place is occupied, then the person who gets on the bus takes the first available seat. Find the probability that the passenger who got on the bus last will take his seat according to his ticket?

A fair dice is thrown many times. It is known that at some point the total amount of points became equal to exactly 2010.

Find the mathematical expectation of the number of throws made to this point.

A fly moves from the origin only to the right or upwards along the lines of the integer grid (a monotonic wander). In each node of the net, the fly randomly selects the direction of further movement: upwards or to the right.

a) Prove that sooner or later the fly will reach the point with abscissa 2011.

b) Find the mathematical expectation of the ordinate of the fly at the moment when the fly reached the abscissa 2011.