Problems
On a calculator, there are numbers from 0 to 9 and signs of two actions (see the figure). First, the display shows the number 0. You can press any key. The calculator performs the actions in the sequence of clicks. If the action sign is pressed several times, the calculator will only remember the last push. The Scattered Scientist pressed a lot of buttons in a random sequence. Find approximately the probability with which the outcome of the resulting chain of actions is an odd number?
Peter and 9 other people play such a game: everyone rolls a dice. The player receives a prize if he or she rolled a number that no one else was able to roll.
a) What is the probability that Peter will receive a prize?
b) What is the probability that at least someone will receive a prize?
The television game “What? Where? When?” consists of a team of “experts” trying to solve 13 questions that are thought up and sent in by the viewers of the program. Envelopes with the questions are selected in turn in a random order with the help of a spinning top with an arrow. If the experts answer correctly, they earn a point, and if they answer incorrectly, the viewers get one point. The game ends as soon as one of the teams scored 6 points. Suppose that the abilities of the teams of experts and viewers are equal.
a) Find the mathematical expectation of the number of points scored by the team of experts in 100 games.
b) Find the probability that, in the next game, envelope number 5 will come up.
James bought \(n\) pairs of identical socks. For \(n\) days James did not have any problems: every morning he took a new pair of socks out of the closet and wore it all day. After \(n\) days, James’ father washed all of the socks in the washing machine and put them into pairs in any way possible as, we repeat, all of the socks are the same. Let’s call a pair of socks successful, if both socks in this pair were worn by James on the same day.
a) Find the probability that all of the resulting pairs are successful.
b) Prove that the expectation of the number of successful pairs is greater than 0.5.
On a laundry drying line \(n\) socks hang in a random order (the order in which they got out of the washing machine). Among them there are the two favourite socks of the Scattered Scientist. The socks are covered by a drying sheet, so the Scientist does not see them, and takes out one sock by touch. Find the mathematical expectation of the number of socks taken out by the Scientist by the time he has both of his favourite socks.
\(N\) pairs of socks hang on a washing line in a random order (the order in which they were taken out of the washing machine). There are no two identical pairs. The socks hang under the drying sheet, so the Scattered Scientist takes out one toe by touch and compares each new sock with all of the previous ones. Find the mathematical expectation of the number of socks taken at the moment when the Scientist will have some pair.
The figure shows a payment order to pay an electricity bill to some power supply company for March 2013.
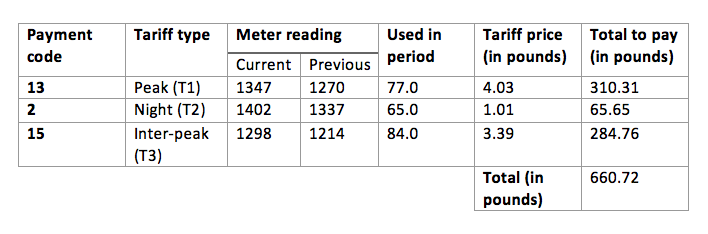
Every month, the client sends the company the testimony of a three-tariff meter installed her the apartment. From the indications for the current month, the corresponding indications for the previous month are subtracted, and the actual monthly expenditure is obtained for each of the three tariff zones (peak, night, inter-peak). Then the expense for each zone is multiplied by the price of one kilowatt-hour in this zone. Adding the received amounts, the client receives the total amount of payment for a month. In this example, the customer will pay £660.72.
The company maintains a record of electricity consumption and payment, using the data received from the customer. The problem is that the company sometimes confuses the six numbers obtained, rearranging them in an arbitrary order, however, it ensures that the current reading remains greater than the previous one. As a result, the calculation of the company may be flawed. If the company believes that the client must pay more than she has paid, the company requires additional payment.
Using the data from the receipt shown, find:
a) the maximum possible amount of surcharge for March 2013, which the company will require from the client;
b) the mathematical expectation of the difference between the amount that the company calculates and the amount paid by the client.
Every day, Patrick the dog chews one slipper from the available stock in the house. Strictly with a probability of 0.5 Patrick wants to chew the left slipper, and with a probability of 0.5 – the right one. If the desired slippers are not present, Patrick becomes upset. How many pairs of the same slippers need to be bought, so that with a probability of not less than 0.8 Patrick does not get upset for an entire week (7 days)?
Find the probability that heads will fall an even number of times, in an experiment in which:
a) a symmetrical coin is thrown \(n\) times;
b) a coin is thrown \(n\) times, for which the probability of getting heads in one throw is \(p(0 < p < 1)\).
In Anchuria, presidential elections are being prepared, in which President Miraflores wants to win. Exactly half of the voters support Miraflores, and the other half support Dick Maloney. Miraflores is also a voter. According to the law, he has the right to divide all of the voters into two constituencies at his own discretion. In each of the districts, the voting is conducted as follows: each voter marks the name of their candidate on the ballot; all ballots are placed in the ballot box. Then one random ballot is chosen from the ballot box, and the one whose name is marked on it will win in this district. The candidate wins the election only if he wins in both districts. If the winner does not appear, the next round of voting is appointed according to the same rules. How should Miraflores divide the electorate in order to maximize the probability of his victory on the first round?