Problems
Author: V.A. Popov
On the interval \([0; 1]\) a function \(f\) is given. This function is non-negative at all points, \(f (1) = 1\) and, finally, for any two non-negative numbers \(x_1\) and \(x_2\) whose sum does not exceed 1, the quantity \(f (x_1 + x_2)\) does not exceed the sum of \(f (x_1)\) and \(f (x_2)\).
a) Prove that for any number \(x\) on the interval \([0; 1]\), the inequality \(f (x_2) \leq 2x\) holds.
b) Prove that for any number \(x\) on the interval \([0; 1]\), the \(f (x_2) \leq 1.9x\) must be true?
The triangle \(C_1C_2O\) is given. Within it the bisector \(C_2C_3\) is drawn, then in the triangle \(C_2C_3O\) – bisector \(C_3C_4\) and so on. Prove that the sequence of angles \(\gamma_n = C_{n + 1}C_nO\) tends to a limit, and find this limit if \(C_1OC_2 = \alpha\).
A rectangular chocolate bar size \(5 \times 10\) is divided by vertical and horizontal division lines into 50 square pieces. Two players are playing the following game. The one who starts breaks the chocolate bar along some division line into two rectangular pieces and puts the resulting pieces on the table. Then players take turns doing the same operation: each time the player whose turn it is at the moment breaks one of the parts into two parts. The one who is the first to break off a square slice \(1\times 1\) (without division lines) a) loses; b) wins. Which of the players can secure a win: the one who starts or the other one?
What has a greater value: \(300!\) or \(100^{300}\)?
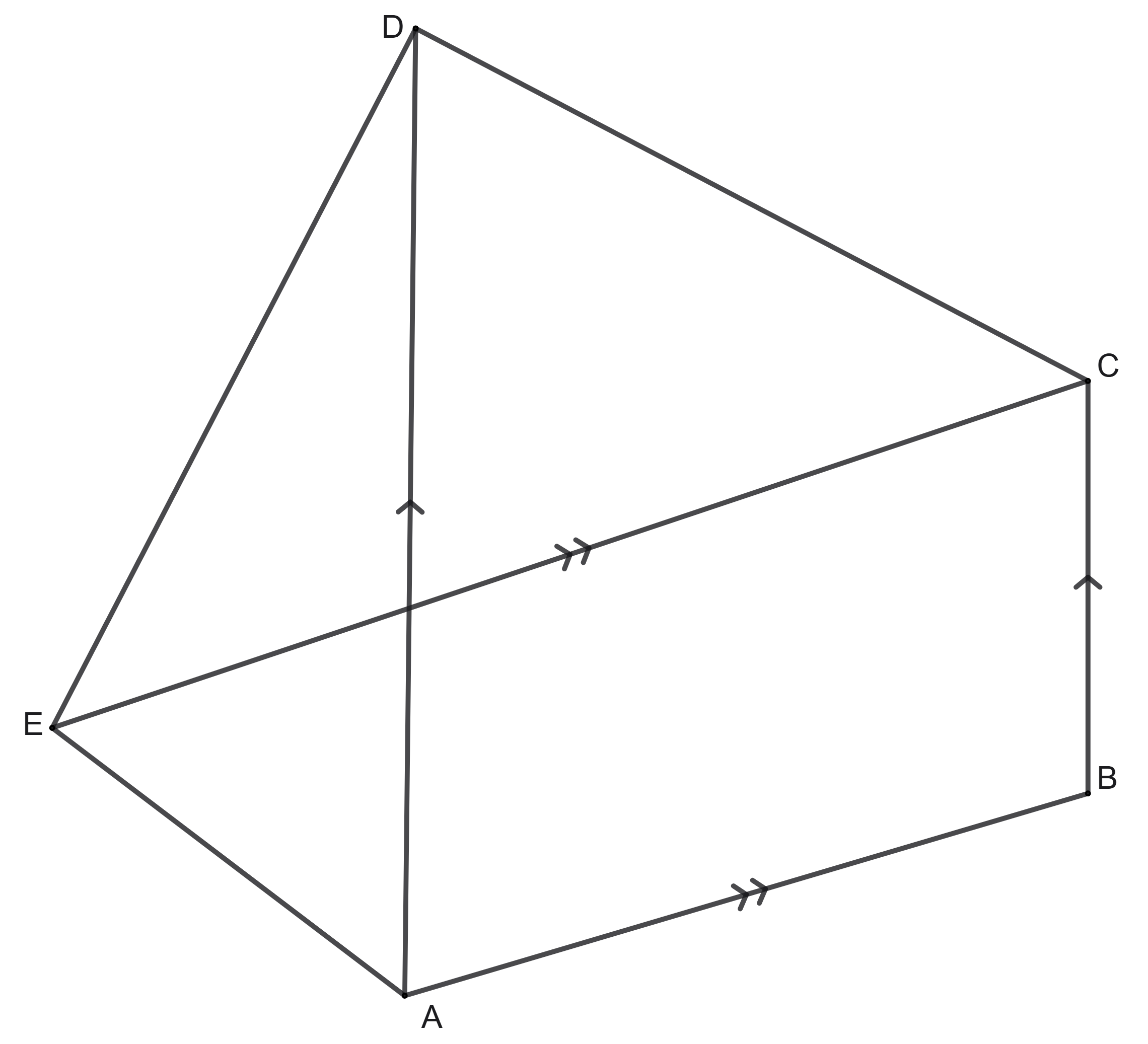
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
If we are given any 100 whole numbers then amongst them it is always possible to choose one, or several of them, so that their sum gives a number divisible by 100. Prove that this is the case.
The equations \[ax^2 + bx + c = 0 \tag{1}\] and \[- ax^2 + bx + c \tag{2}\] are given. Prove that if \(x_1\) and \(x_2\) are, respectively, any roots of the equations (1) and (2), then there is a root \(x_3\) of the equation \(\frac 12 ax^2 + bx + c\) such that either \(x_1 \leq x_3 \leq x_2\) or \(x_1 \geq x_3 \geq x_2\).
The expression \(ax^2+bx+c\) is an exact fourth power for all integers \(x\). Prove that \(a=b=0\).
The numbers \(\lfloor a\rfloor, \lfloor 2a\rfloor, \dots , \lfloor Na\rfloor\) are all different, and the numbers \(\lfloor 1/a\rfloor, \lfloor 2/a\rfloor,\dots , \lfloor M/a\rfloor\) are also all different. Find all such \(a\).
2022 points are selected from a cube, whose edge is equal to 13 units. Is it possible to place a cube with edge of 1 unit in this cube so that there is not one selected point inside it?