Problems
Ben noticed that all 25 of his classmates have a different number of friends in this class. How many friends does Ben have?
A village infant school has \(20\) pupils. If we pick any two pupils, then they will have a shared granddad.
Prove that one of the granddads has at least \(14\) grandchildren who are pupils at this school.
Some points with integer coordinates are marked on a plane. It is known that no four of the marked points lie on the same circumference of a circle (that is, no circle passes through four of them). Prove that there exists a circle of radius \(1995\) whose circumference contains none of the marked points.
Let \(n\) numbers are given together with their product \(p\). The difference between \(p\) and each of these numbers is an odd number.
Prove that all \(n\) numbers are irrational.
In a regular polygon with \(25\) vertices, all the diagonals are drawn.
Prove that there are no nine diagonals passing through one interior point of the shape.
A group of psychologists developed a test, after which each person gets a mark, the number \(Q\), which is the index of his or her mental abilities (the greater \(Q\), the greater the ability). For the country’s rating, the arithmetic mean of the \(Q\) values of all of the inhabitants of this country is taken.
a) A group of citizens of country \(A\) emigrated to country \(B\). Show that both countries could grow in rating.
b) After that, a group of citizens from country \(B\) (including former ex-migrants from \(A\)) emigrated to country \(A\). Is it possible that the ratings of both countries have grown again?
c) A group of citizens from country \(A\) emigrated to country \(B\), and group of citizens from country \(B\) emigrated to country \(C\). As a result, each country’s ratings was higher than the original ones. After that, the direction of migration flows changed to the opposite direction – part of the residents of \(C\) moved to \(B\), and part of the residents of \(B\) migrated to \(A\). It turned out that as a result, the ratings of all three countries increased again (compared to those that were after the first move, but before the second). (This is, in any case, what the news agencies of these countries say). Can this be so (if so, how, if not, why)?
(It is assumed that during the considered time, the number of citizens \(Q\) did not change, no one died and no one was born).
Daniel has drawn on a sheet of paper a circle and a dot inside it. Show that he can cut a circle into two parts which can be used to make a circle in which the marked point would be the center.
Elon is studying the Twitter server. Inside the software he found two integer variables \(a\) and \(b\) which change their values when special search queries “RED”, “GREEN”, and “BLUE” are processed. More precisely the pair \((a, b)\) changes into \((a + 18b, 18a - b)\) when processing the query “RED”, to \((17a + 6b, -6a + 17b)\) when processing “GREEN”, and to \((-10a - 15b, 15a - 10b)\) when processing “BLUE”. When any of \(a\) or \(b\) reaches a multiple of \(324\), it resets to \(0\). If \((a, b) = (0, 0)\) the server crashes. On the server startup, the variables \((a, b)\) are set to \((20, 20)\). Prove that the server will never crash with these initial values, regardless of the search queries processed.
Is it possible to cut an equilateral triangle into three equal hexagons?
A labyrinth was drawn on a \(5\times
5\) grid square with an outer wall and an exit one cell wide, as
well as with inner walls running along the grid lines. In the picture,
we have hidden all the inner walls from you (We give you several copies
to facilitate drawing) 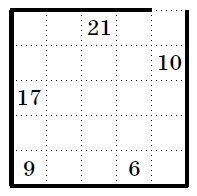


Please draw how the walls were arranged. Keep in mind that the numbers
in the cells represent the smallest number of steps needed to exit the
maze, starting from that cell. A step can be taken to any adjacent cell
vertically or horizontally, but not diagonally (and only if there is no
wall between them, of course).