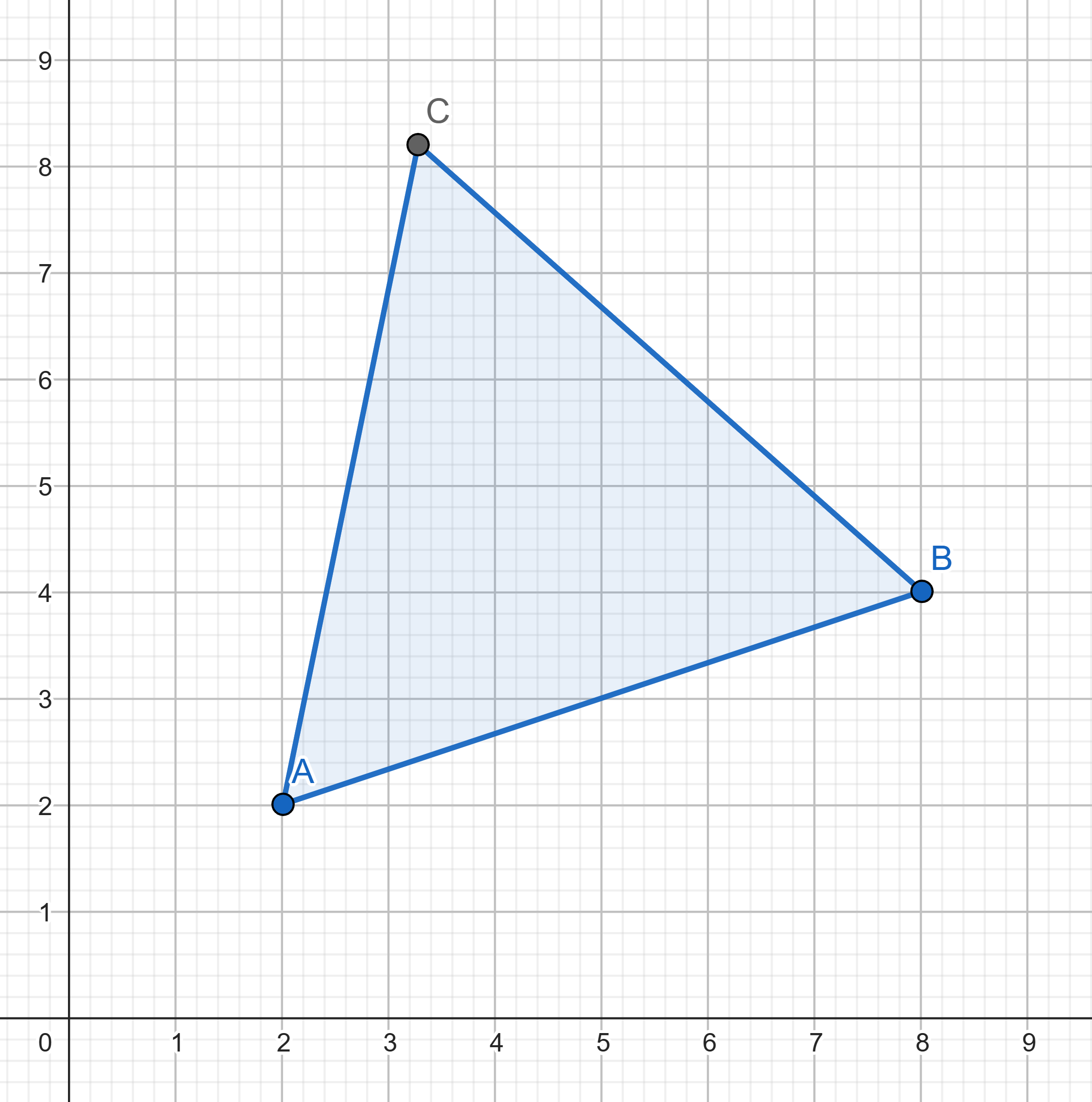
Problems
Can three points with integer coordinates be the vertices of an
equilateral triangle?
Prove that there are infinitely many prime numbers \(\{2,3,5,7,11,13...\}\).
A rectangular parallelepiped of the size \(m\times n\times k\) is divided into unit cubes. How many rectangular parallelepipeds are formed in total (including the original one)?
The dragon locked six dwarves in the cave and said, "I have seven caps of the seven colors of the rainbow. Tomorrow morning I will blindfold you and put a cap on each of you, and hide one cap. Then I’ll take off the blindfolds, and you can see the caps on the heads of others, but not your own and I won’t let you talk any more. After that, everyone will secretly tell me the color of the hidden cap. If at least three of you guess right, I’ll let you all go. If less than three guess correctly, I’ll eat you all for lunch." How can dwarves agree in advance to act in order to be saved?
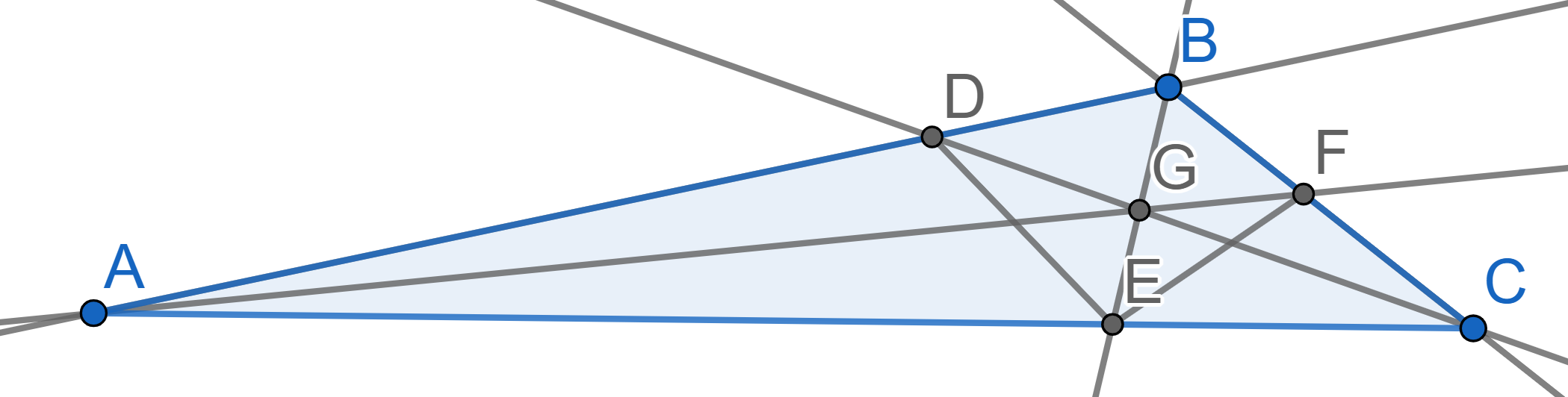
In the triangle \(ABC\) the angle
\(\angle ABC = 120^{\circ}\). The
segments \(AF,\, BE\), and \(CD\) are the bisectors of the corresponding
angles of the triangle \(ABC\). Prove
that the angle \(\angle DEF =
90^{\circ}\).
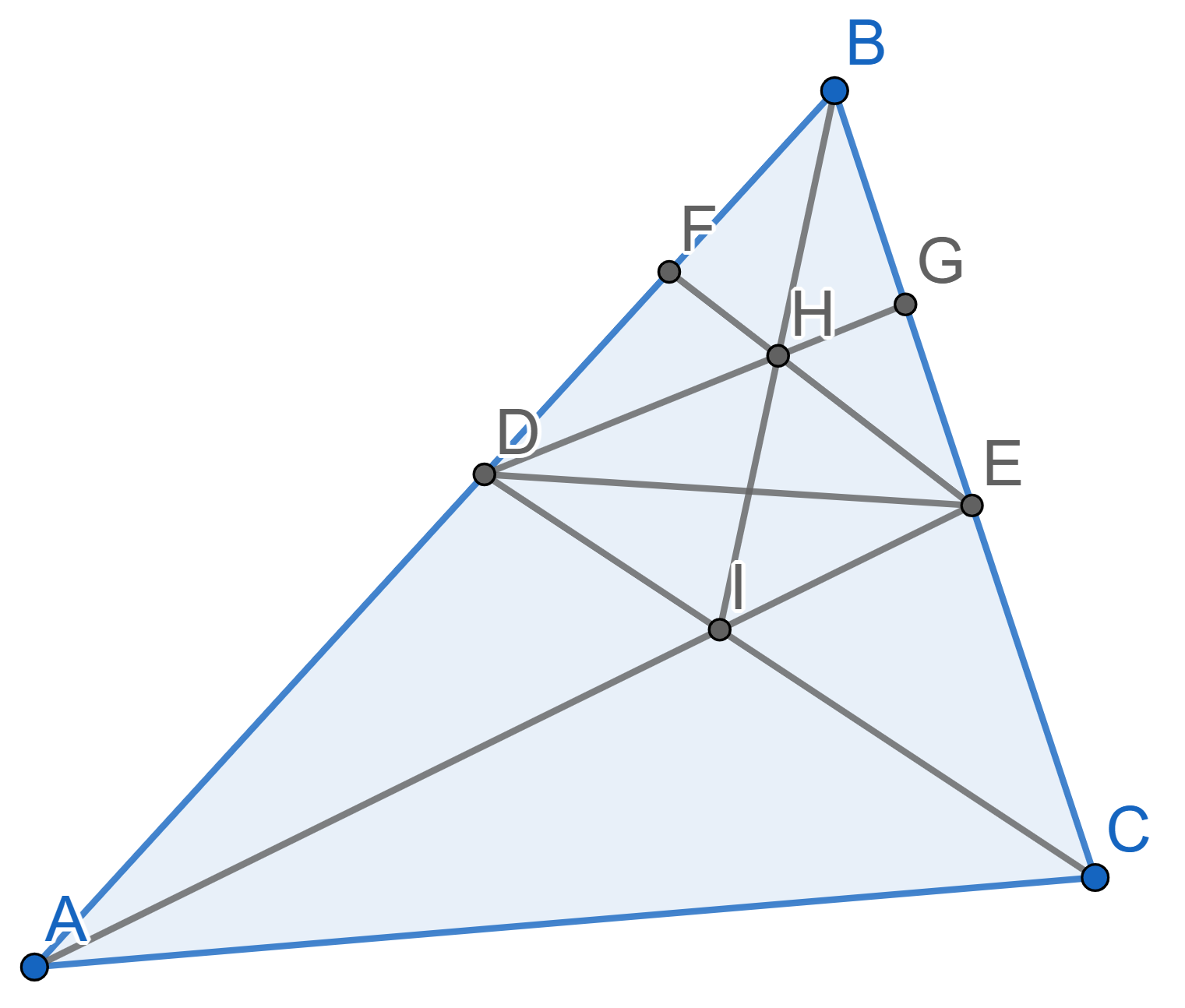
In the triangle \(ABC\) the lines
\(AE\) and \(CD\) are the bisectors of the angles \(\angle BAC\) and \(\angle BCA\), intersecting at the point
\(I\). In the triangle \(BDE\) the lines \(DG\) and \(EF\) are the bisectors of the angles \(\angle BDE\) and \(\angle BED\), intersecting at the point
\(H\). Prove that the points \(B,\,H,\, I\) are situated on one straight
line.
Jess and Tess are playing a game colouring points on a blank plane. Jess is moving first, she picks a non-colored point on a plane and colours it red. Then Tess makes a move, she picks \(2022\) colourless points on the plane and colours them all green. Jess then moves again, and they take turns. Jess wins if she manages to create a red equilateral triangle on the plane, Tess is trying to prevent that from happening. Will Jess always eventually win?
Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?
A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:
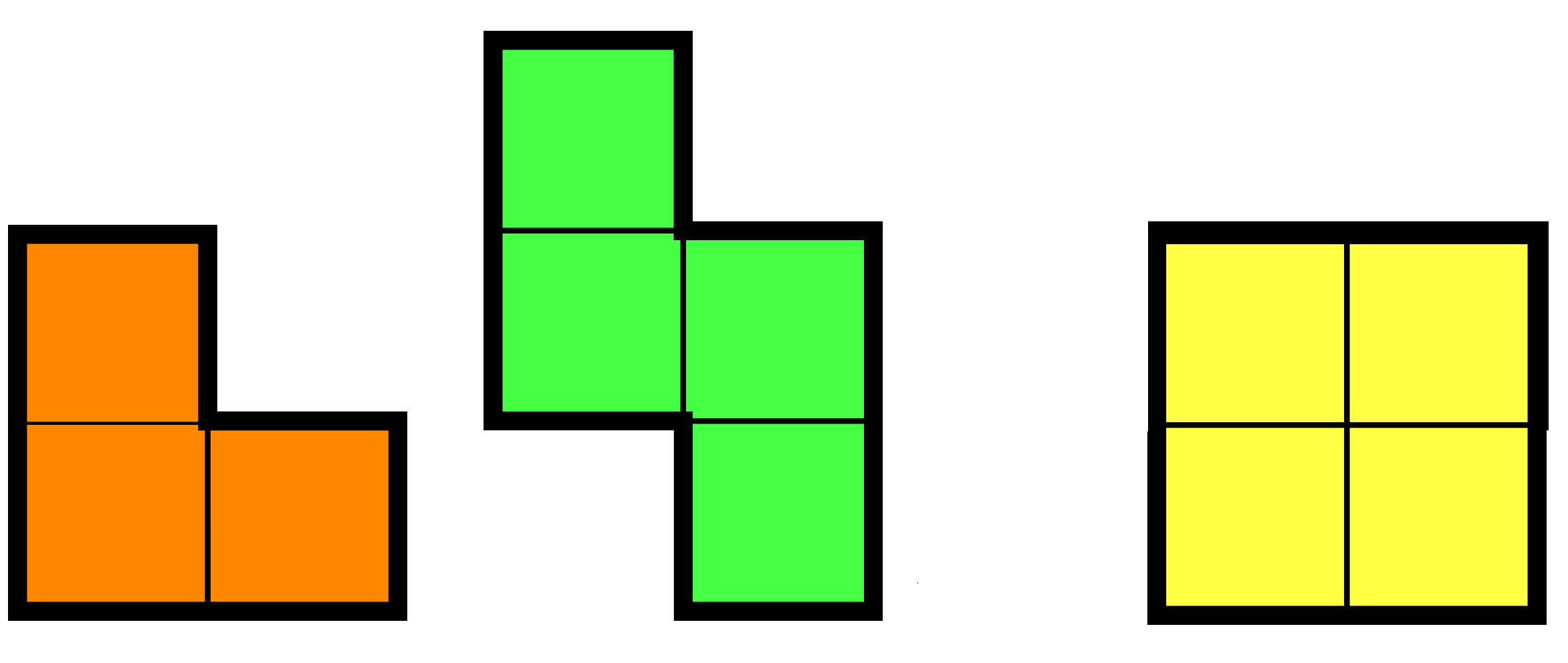
Prove that at least \(4n-1\) of the first type have been used.
Alice the fox and Basilio the cat have grown \(20\) counterfeit bills on a money tree and now write seven-digit numbers on them. Each bill has \(7\) empty cells for numbers. Basilio calls out one digit "1" or "2" (he doesn’t know the others), and Alice writes the number into any empty cell of any bill and shows the result to Basilio. When all the cells are filled, Basilio takes as many bills with different numbers as possible (out of several with the same number, he takes only one), and the rest is taken by Alice. What is the largest number of bills Basilio can get, regardless of Alice’s actions?