Problems

Detective Nero Wolf investigates a crime. He’s got \(80\) people involved in the case, among whom one is a criminal and another is a witness to the crime (but it is not known who either of them are). Each day the detective may invite one or more of these \(80\) people, and if there is a witness among those invited, but not the perpetrator, the witness will report who the perpetrator is. Can the detective solve a case in \(12\) days?

Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.

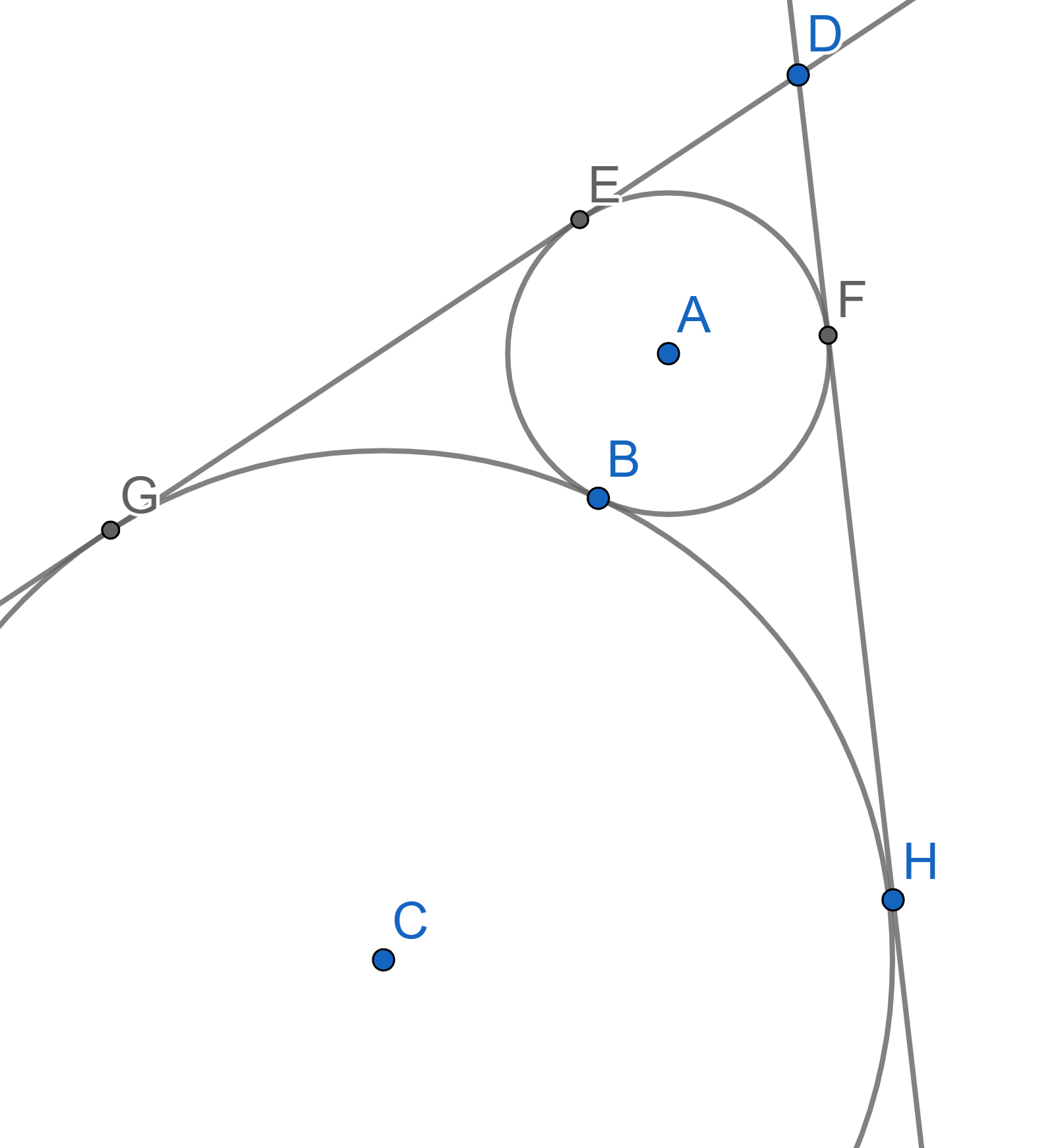
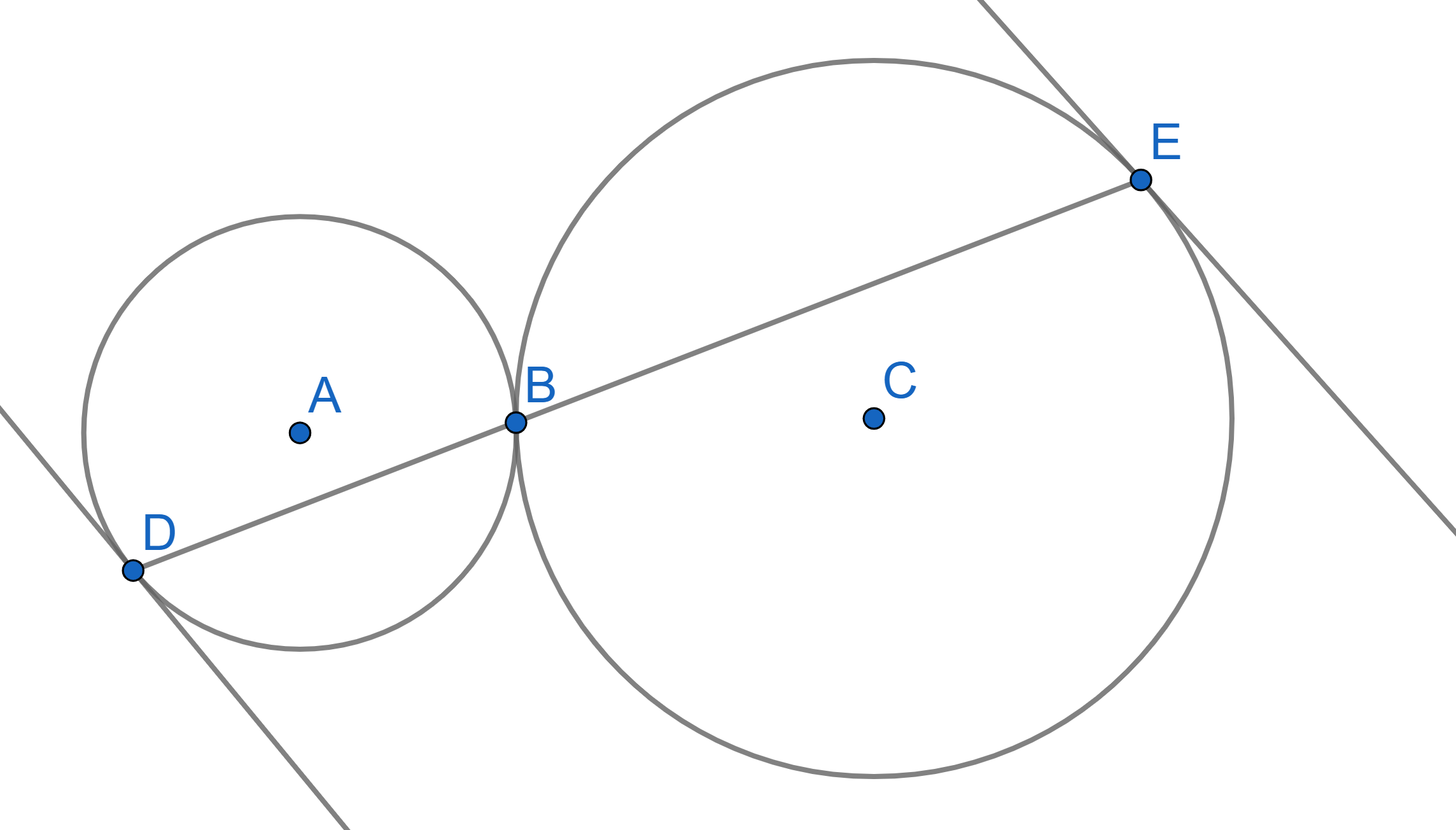
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).

The number \(n\) is natural. Show that: \[\frac1{\sqrt{1}} +\frac1{\sqrt{2}}+ \frac1{\sqrt{3}} + \dots +\frac1{\sqrt{n}} < 3 \sqrt{n+1} -3.\]

If \(n\) is a positive integer, we denote by \(s(n)\) the sum of the divisors of \(n\). For example, the divisors of \(n=6\) are \(1,2,3,6\), so \(s(6)=1+2+3+6=12\). Prove that, for all \(n\geq1\), \[s(1)+s(2)+\cdots+s(n)\leq n^2.\] Denote by \(t(n)\) is instead the sum of the squares of the divisors of \(n\) (e.g., \(t(6)=1^2+2^2+3^2+6^2=50\)), can you find a similar inequality for \(t(n)\)?

There are \(16\) cities in the kingdom. We would like to build roads between these cities so that one can get from any city to any other without passing through more than one city on the way. To save cost, we would like to have no more than four roads coming out of each city. Prove that such a system of roads is unfortunately impossible to build.

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

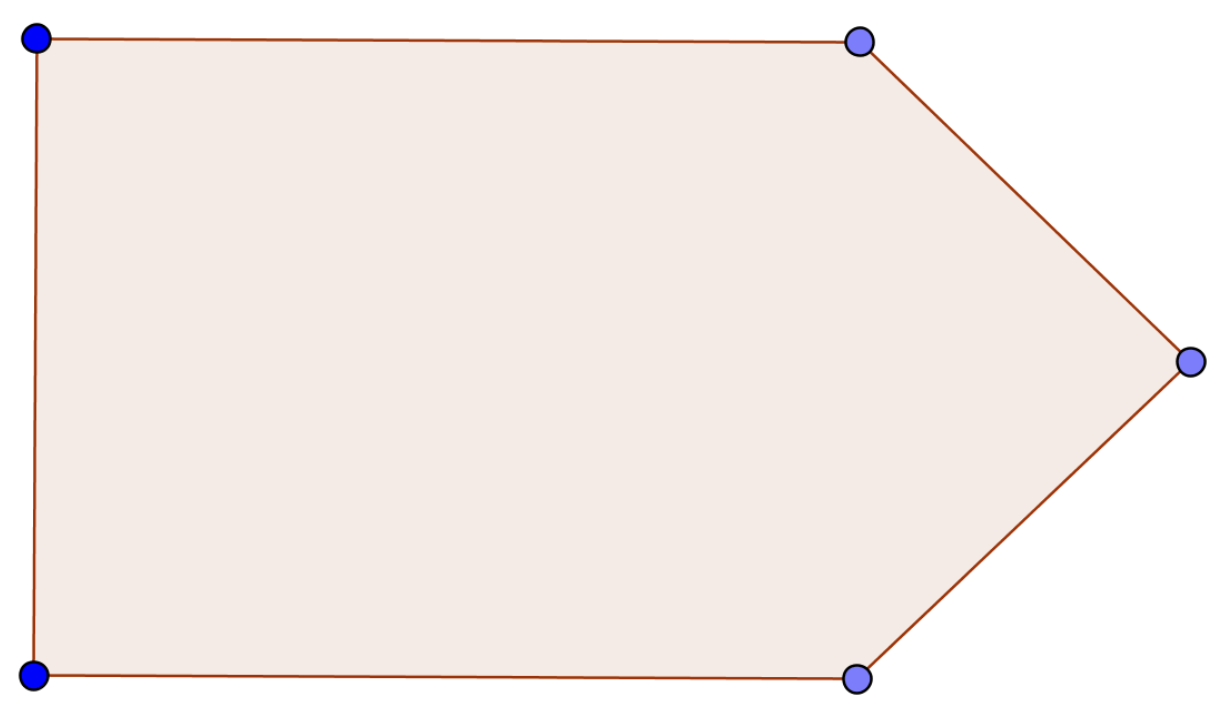
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.