Problems
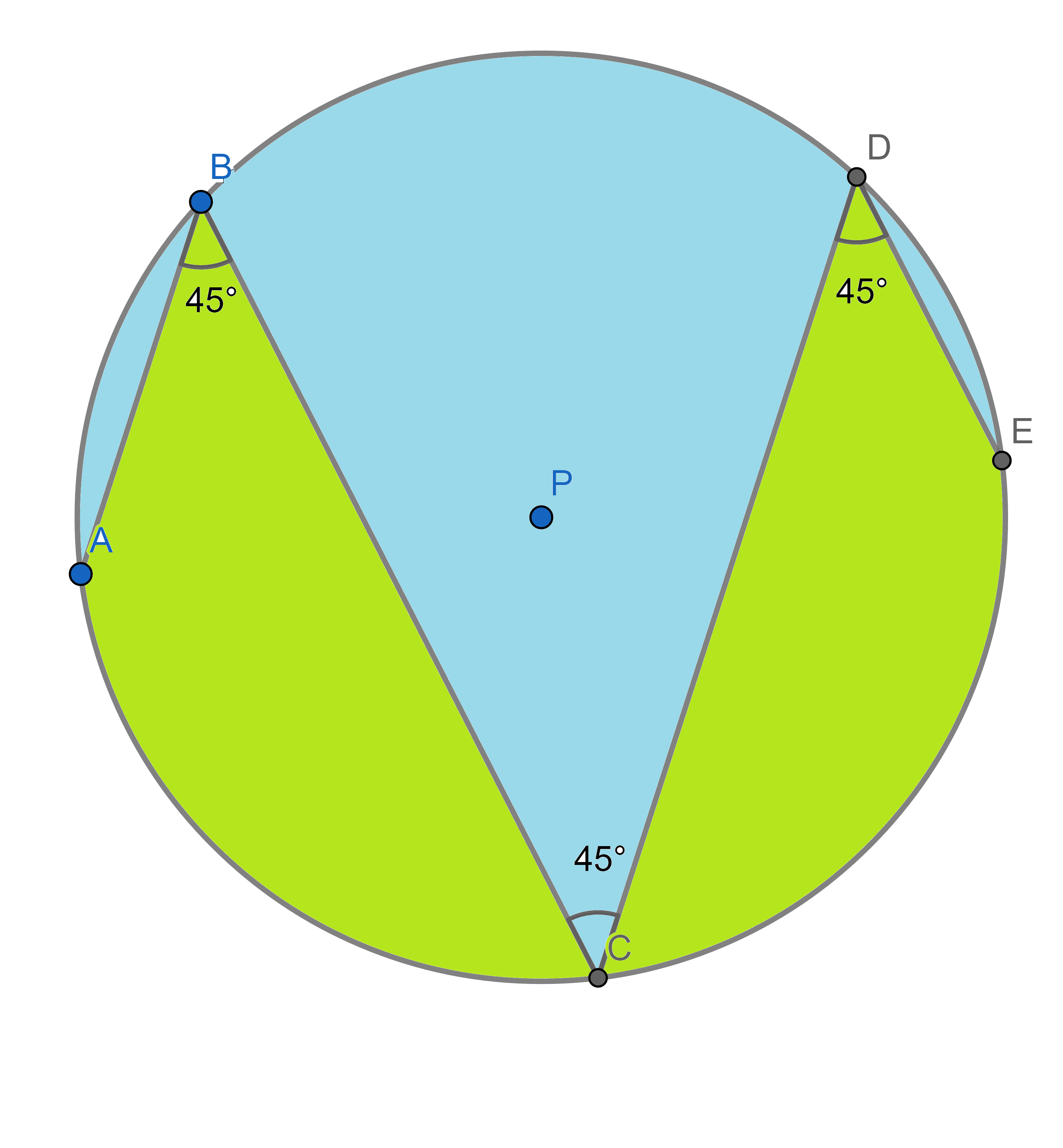
The marked angles are all \(45^{\circ}\). Show that the total green and blue areas are the same.
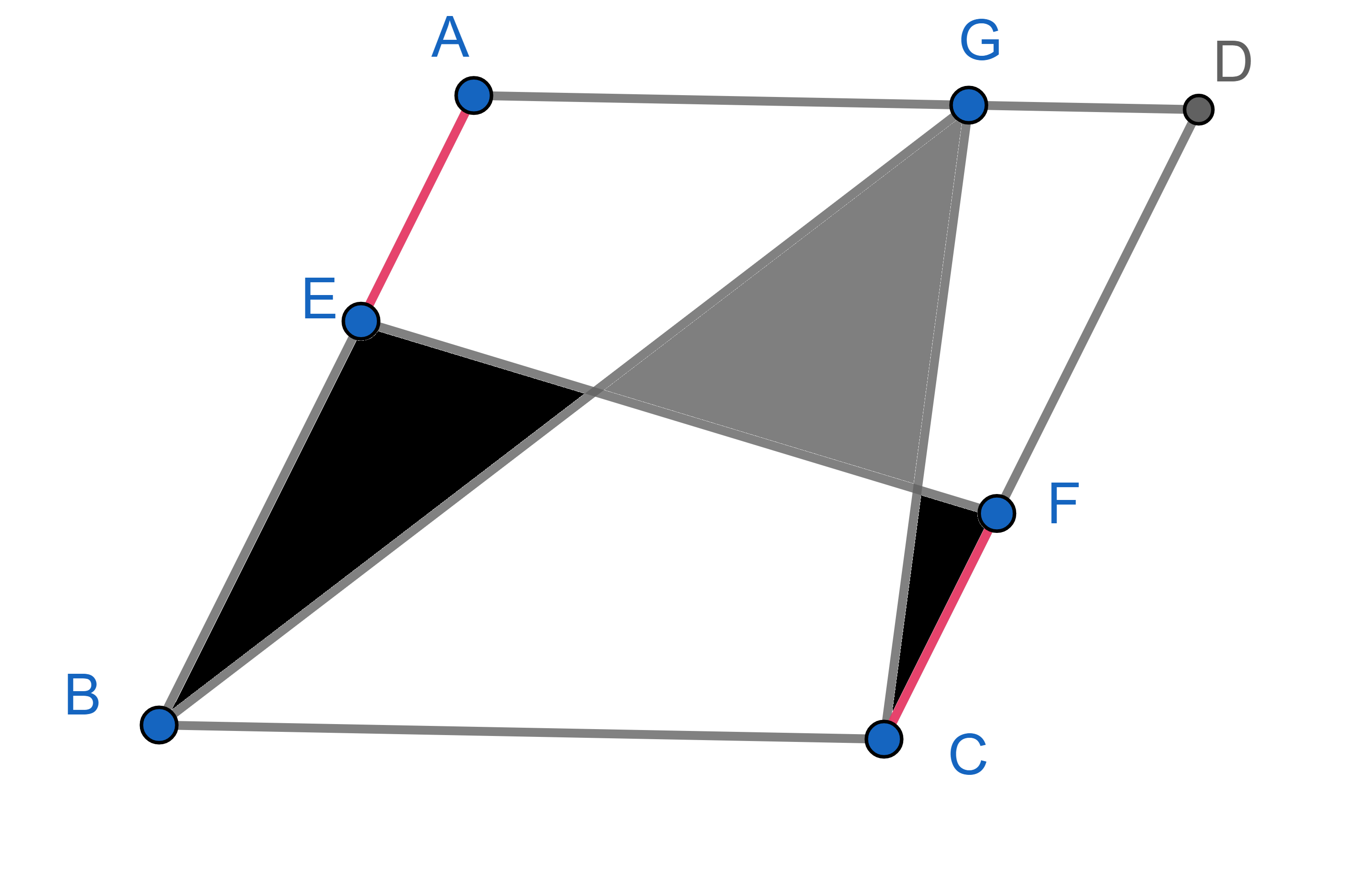
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). We know that the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.
Jamie’s drawer is pretty big. It has infinitely many crayons. In
fact, for every colour of crayon, there are infinitely many crayons of
that colour.
In every group of \(9\) randomly chosen
crayons from Jamie’s drawer, some \(3\)
will have the same colour. Jamie chooses \(25\) crayons at random. Prove that some
\(7\) of them will have the same
colour.
Suppose \(n \ge 2\) cricket teams play in a tournament. No two teams play each other more than once, and no team plays itself. Prove that some two teams have to play the same number of games.
Find all the prime numbers \(p\) such that there exist natural numbers \(x\) and \(y\) for which \(p^x = y^3 + 1\).
Find all natural numbers \(n\) for which there exist integers \(a,b,c\) such that \(a+b+c = 0\) and the number \(a^n + b^n + c^n\) is prime.
On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?
There is a scout group where some of the members know each other. Amongst any four members there is at least one of them who knows the other three. Prove that there is at least one member who knows the entirety of the scout group.
The distance between two villages equals \(999\) kilometres. When you go from one village to the other, every kilometre you see a sign on the road, saying \(0 \mid 999, \, 1\mid 998, \, 2\mid 997, ..., 999\mid 0\). The signs show the distances to the two villages. Find the number of signs that contain only two different digits. For example, the sign \(0\mid999\) contains only two digits, namely \(0\) and \(9\), whereas the sign \(1\mid998\) contains three digits, namely \(1\), \(8\) and \(9\).
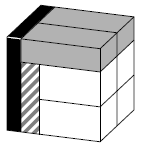
Michael made a cube with edge \(1\) out of eight bars as in the picture. All \(8\) bars have the same volume. The dimensions of the grey bars are the same as each other. Similarly, the dimensions of the white bars are the same as each other. Find the lengths of the edges of the white bars.