Problems
Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.
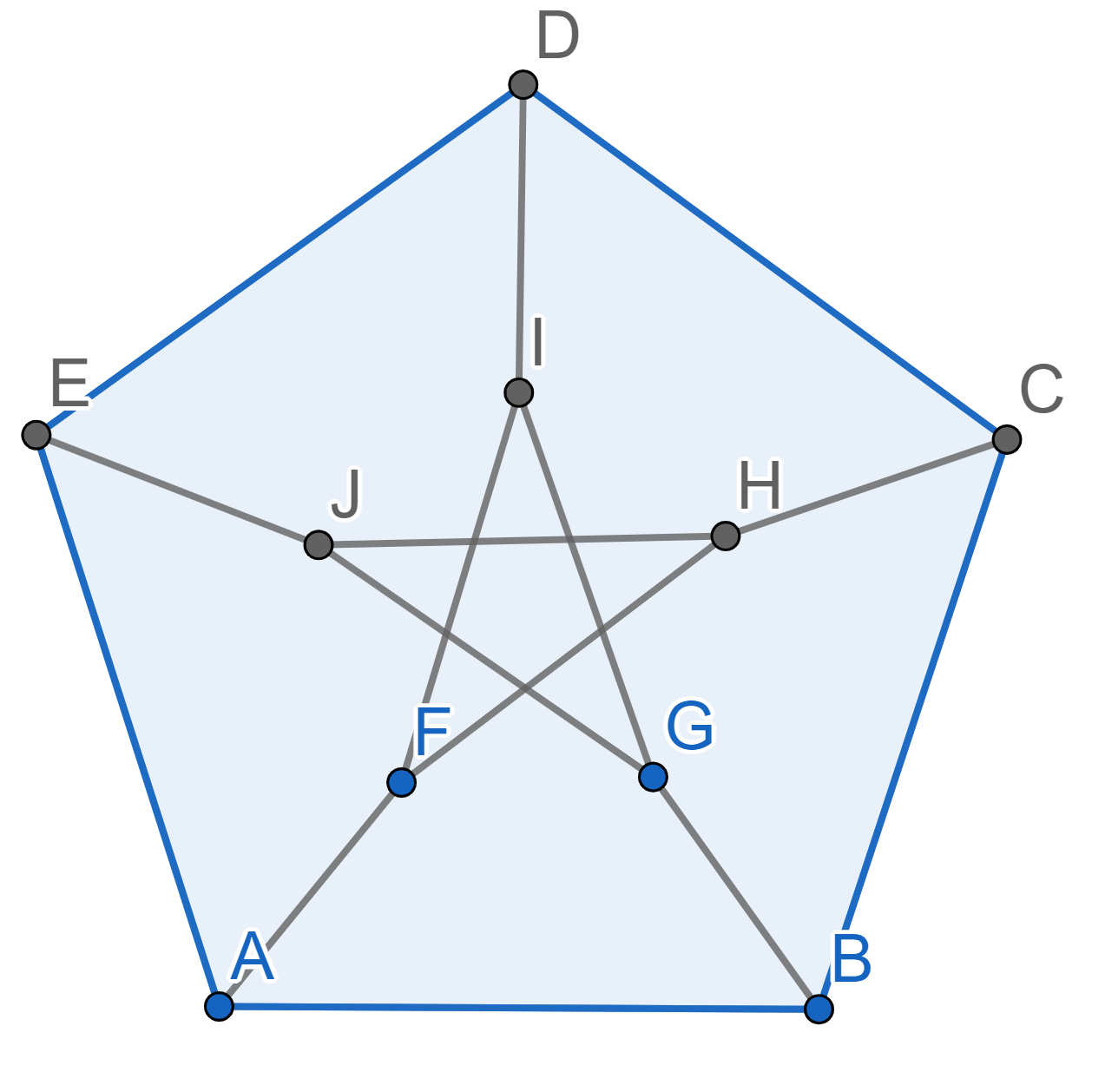
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?
In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?
An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.
Split the numbers from \(1\) to \(9\) into three triplets such that the sum of the three numbers in each triplet is prime. For example, if you split them into \(124\), \(356\) and \(789\), then the triplet \(124\) is correct, since \(1+2+4=7\) is prime. But the other two triples are incorrect, since \(3+5+6=14\) and \(7+8+9=24\) are not prime.
A family is going on a big holiday, visiting Austria, Bulgaria, Cyprus, Denmark and Estonia. They want to go to Estonia before Bulgaria. How many ways can they visit the five countries, subject to this constraint?
Let \(p\), \(q\) and \(r\) be distinct primes at least \(5\). Can \(p^2+q^2+r^2\) be prime? If yes, then give an example. If no, then prove it.
How many subsets of \(\{1,2,...,n\}\) (that is, the integers from \(1\) to \(n\)) have an even product? For the purposes of this question, take the product of the numbers in the empty set to be \(1\).
How many subsets are there of \(\{1,2,...,n\}\) (the integers from \(1\) to \(n\) inclusive) containing no consecutive
digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have
\(8\) subsets overall but only \(5\) contain no consecutive integers. The
\(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three
of these.
Let \(A\), \(B\), \(C\) and \(D\) be four points labelled clockwise on the circumference of a circle. The diagonals \(AC\) and \(BD\) intersect at the centre \(O\) of the circle. What can be deduced about the quadrilateral \(ABCD\)?
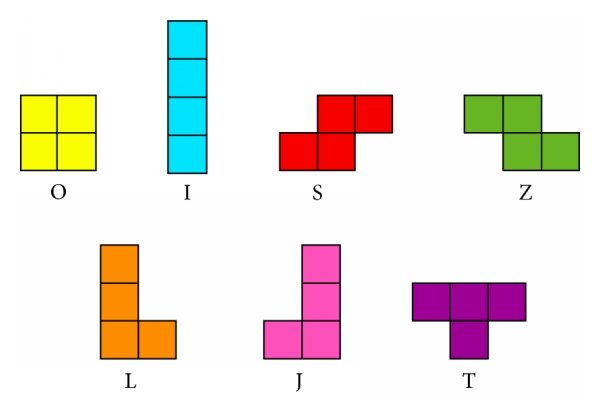
Consider the 7 different tetrominoes. Is it possible to cover a \(4\times7\) rectangle with exactly one copy of each of the tetrominoes? If it is possible, then provide an example layout. If it is not possible, then prove that it’s impossible.
We allow rotation of the tetrominoes, but not reflection. This means that we consider \(S\) and \(Z\) as different, as well as \(L\) and \(J\).