Problems

You and I are going to play a game. We have one million grains of sand in a bag. We take it in turns to remove \(2\), \(3\) or \(5\) grains of sand from the bag. The first person that cannot make a move loses.

Would you go first?

For every natural number \(k\ge2\), find two combinations of \(k\) real numbers such that their sum is twice their product.

Show that \(n^2+n+1\) is not divisible by \(5\) for any natural number \(n\).

Prove the following identity for any three non-zero real numbers \(a,b,c\): \[\frac{b}{2a} + \frac{c^2 + ab}{4bc} - \left|{\frac{c^2 - ab}{4bc}} \right| - \left|{\frac{b}{2a} - \frac{c^2 + ab}{4bc} + \left|{\frac{c^2 - ab}{4bc}}\right|}\right| = \min\{\frac{b}{a},\frac{c}{b},\frac{a}{c}\}.\]

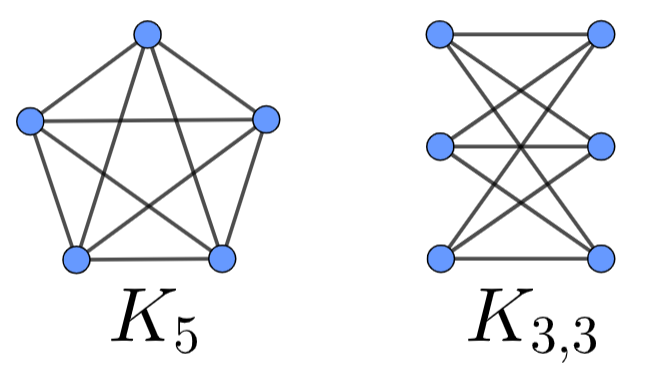
In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on \(3\) and \(3\) vertices. A theorem states that these graphs cannot be embedded into plane, namely one cannot draw graphs \(K_5\) and \(K_{3,3}\) on a plane in such a way that there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a torus?

Is it possible to link three rings together in such a way that they cannot be separate from each other, but if you remove any ring, then the other two will fall apart?

Prove that \(|x|\ge x\). It may be helpful to compare each of \(|3|\), \(|-4.3|\) and \(|0|\) with \(3\), \(-4.3\) and \(0\) respectively.

Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?

There is a triangle with side lengths \(a\), \(b\) and \(c\). Can you form a triangle with side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\) and \(c\) are? Give a proof if it is always possible or never possible. Otherwise, construct examples to show the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\) and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).

There is a triangle with side lengths \(a\), \(b\) and \(c\). Does there exist a triangle with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\) and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\) and \(z\) if and only if all the inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.