Problems

You might want to know what day of the week your birthday is this year. Mathematician John Conway invented an algorithm called the ‘Doomsday Rule’ to determine which day of the week a particular date falls on. It works by finding the ‘anchor day’ for the year that you’re working in. For \(2025\), the anchor day is Friday. Certain days in the calendar always fall on the anchor day. Some memorable ones are the following:
‘\(0\)’ of March - which is \(29\)th February in a leap year, and \(28\)th February otherwise.

\(4\)th April, \(6\)th June, \(8\)th August, \(10\)th October and \(12\)th December. These are easier to remember as \(4/4\), \(6/6\), \(8/8\), \(10/10\) and \(12/12\).

\(9\)th May, \(11\)th July, \(5\)th September and \(7\)th November. These are easier to see as \(9/5\), \(11/7\), \(5/9\) and \(7/11\). A mnemonic for them is “9-5 at the 7-11".
Then find the nearest one of these dates to the date that you’re looking for and find remainders.

For example, \(\pi\) day, (\(14\)th March, which is written \(3/14\) in American date notation. It’s also Albert Einstein’s birthday) is exactly \(14\) days after ‘\(0\)’th March, so is the same day of the week - Friday in \(2025\).

What day of the week will \(25\)th December be in \(2025\)?

\(6\) friends get together for a game of three versus three basketball. In how many ways can they be split into two teams? The order of the two teams doesn’t matter, and the order within the teams doesn’t matter.

That is, we count A,B,C vs. D,E,F as the same splitting as F,D,E vs A,C,B.

\(x\), \(y\) and \(z\) are all integers. We’re told that \[\begin{align} x^3yz&=6\\ xy^3z&=24\\ xyz^3&=54. \end{align}\] What’s \(xyz\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?

Picasso colours every point on the circumference of a circle red or blue. Is he guaranteed to create an equilateral triangle all of whose vertices are the same colour?

Let \(A\), \(B\), \(C\), \(D\), \(E\) be five different points on the circumference of a circle in that (cyclic) order. Let \(F\) be the intersection of chords \(BD\) and \(CE\). Show that if \(AB=AE=AF\) then lines \(AF\) and \(CD\) are perpendicular.

Let \(a\), \(b\) and \(c\) be positive real numbers such that \(a+b+c=3\). Prove that \(a^a+b^b+c^c\ge3\).

David and Esther play the following game. Initially, there are three piles, each containing 1000 stones. The players take turns to make a move, with David going first. Each move consists of choosing one of the piles available, removing the unchosen pile(s) from the game, and then dividing the chosen pile into 2 or 3 non-empty piles. A player loses the game if they are unable to make a move. Prove that Esther can always win the game, no matter how David plays.

Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.

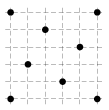
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.