Problems

Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.

Note: a graph is planar if it can be drawn in the plane with no edges crossing. For example, three houses, each of which is connected to three utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).

Two players are playing a game. The first player is thinking of a finite sequence of positive integers \(a_1\), \(a_2\), ..., \(a_n\). The second player can try to find the first player’s sequence by naming their own sequence \(b_1\), \(b_2\), ..., \(b_n\). After this, the first player will give the result \(a_1b_1 + a_2b_2 + ...+a_nb_n\). Then the second player can say another sequence \(c_1\), \(c_2\), ..., \(c_n\) to get another answer \(a_1c_1+ a_2c_2 + ... +a_nc_n\) from the first player. Find the smallest number of sequences the second player has to name to find out the sequence \(a_1\), \(a_2\), ..., \(a_n\).

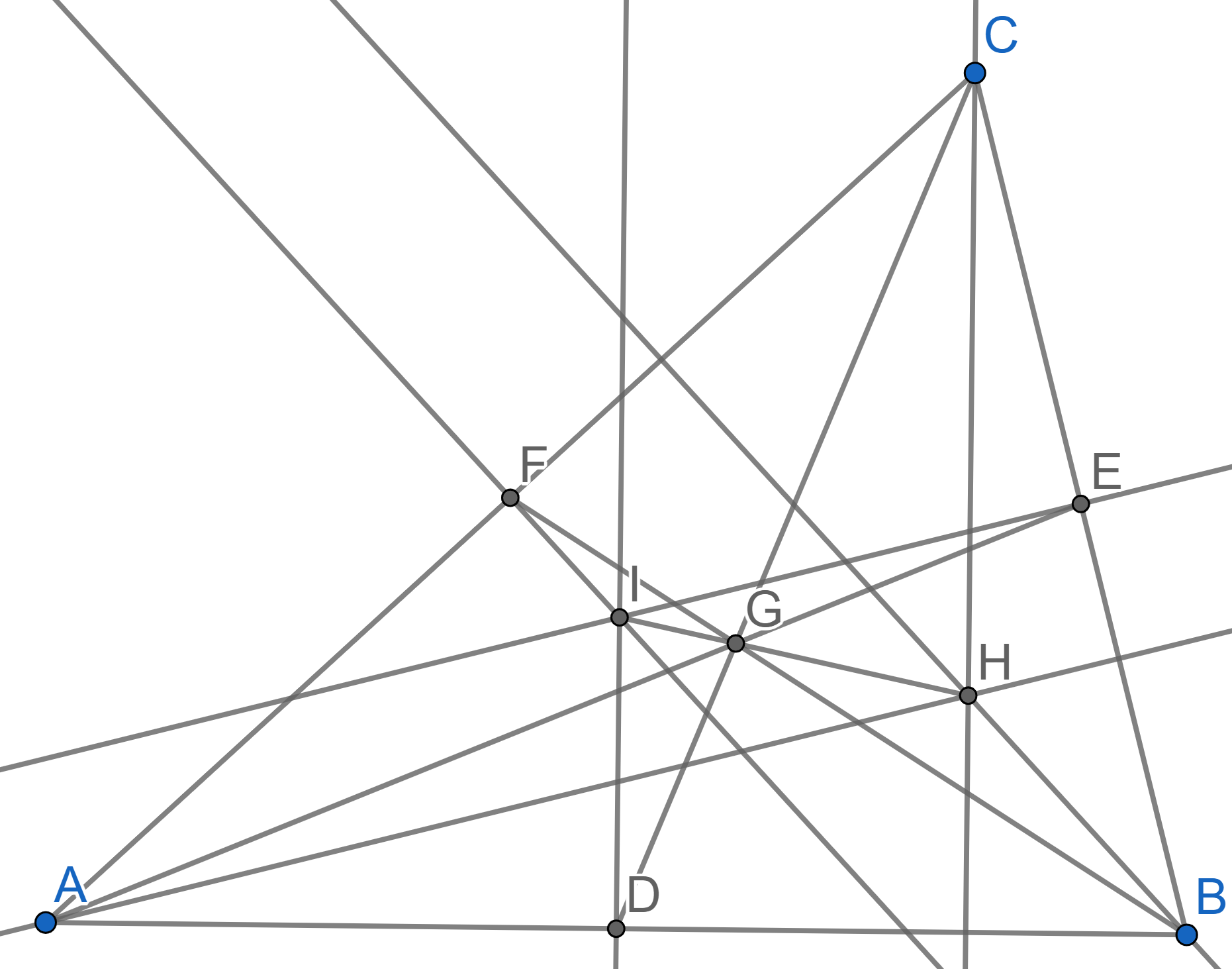
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\). The point \(H\) is the point of intersection of all heights. The point \(I\) is the center of the circumscribed circle of \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and that the ratio \(IG:GH = 1:2\). The line that all of \(I\), \(G\) and \(H\) lie on is called the Euler line of triangle \(ABC\).

Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

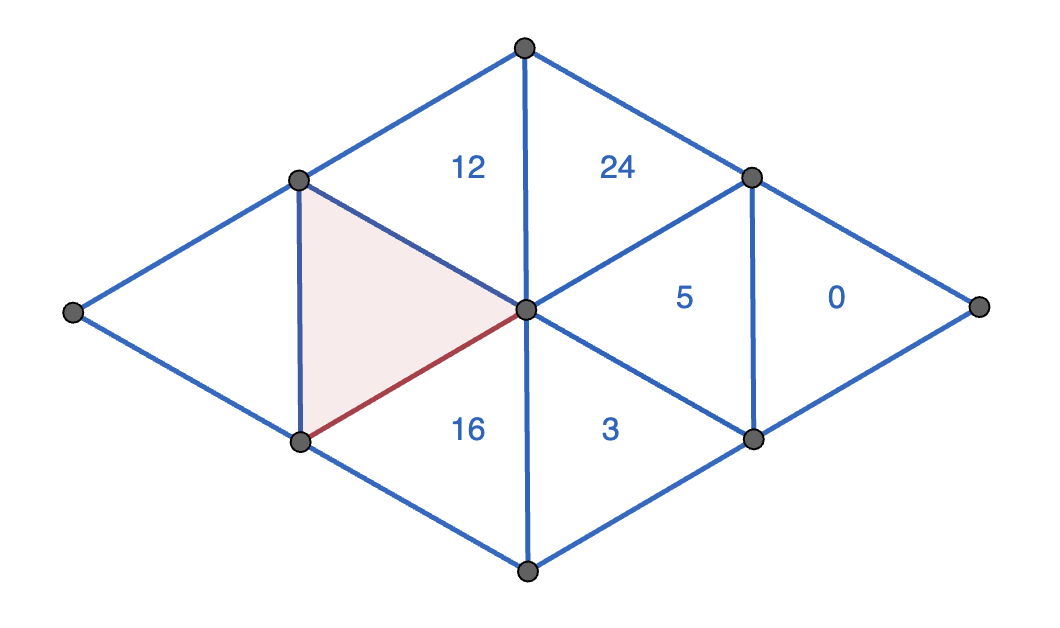
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.

How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

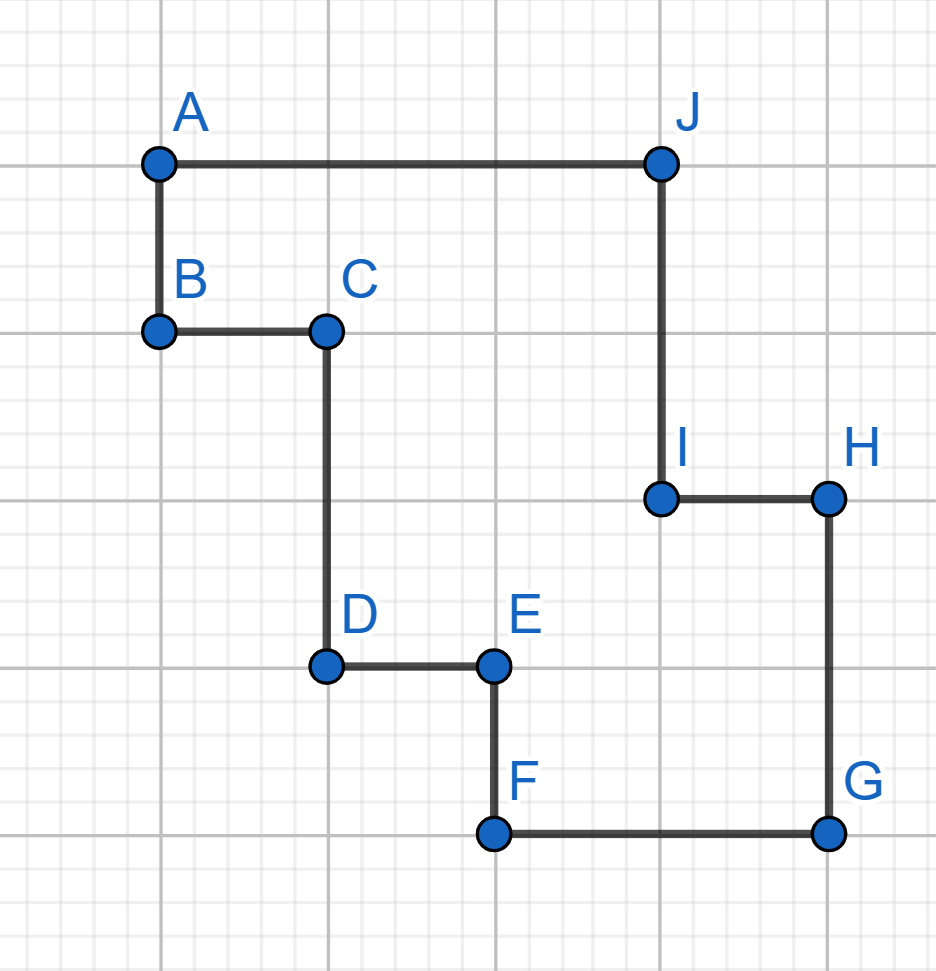
On a sheet of paper a grid of \(n\) horizontal and \(n\) vertical straight lines is drawn. How many different closed \(2n\)-link broken lines can be drawn along the grid lines so that each broken line passes through all horizontal and all vertical straight lines? On the diagram below you can see an example of a closed broken line for \(n = 5\).

Find the largest number \(A\) such that for each permutation of the set \(\{1,2,3, \dots, 100\}\), the sum of some \(10\) consecutive terms of that permutation is at least equal to \(A\).

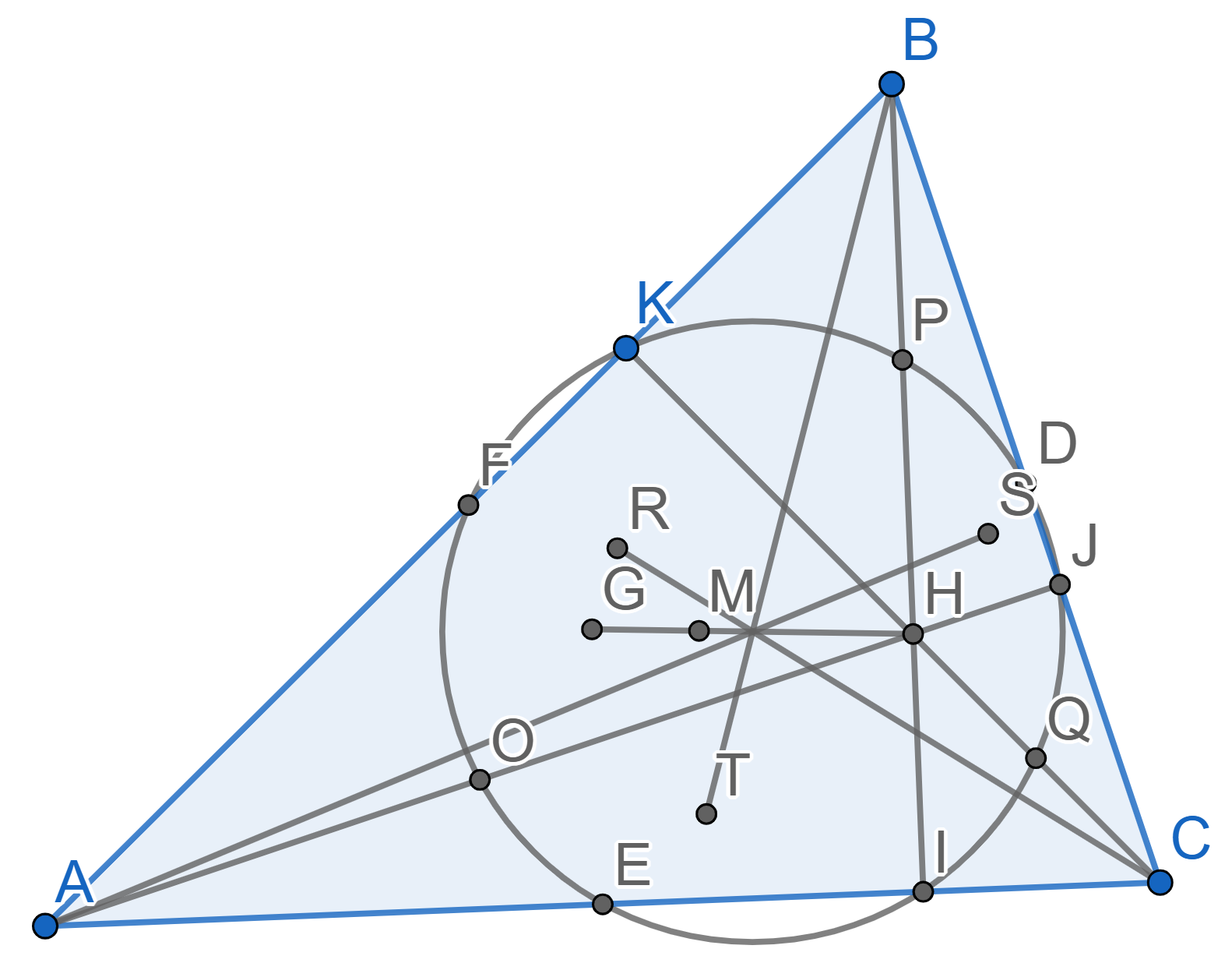
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\) and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\) and let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Consider the Euler circle of the triangle \(ABC\), which is the one that contains the points \(D,J,I,E,F,K\). This circle intersects the segments \(AH\), \(BH\) and \(CH\) at the points \(O\), \(P\) and \(Q\) respectively. Prove that \(O\), \(P\) and \(Q\) are the midpoints of the segments \(AH\), \(BH\) and \(CH\).

Consider the point \(H\) of intersection of the heights of the triangle \(ABC\). Prove that Euler lines of the triangles \(ABC\), \(ABH\), \(BCH\) and \(ACH\) intersect at one point. On the diagram below the points \(R,S,T\) are the points of intersection of medians in triangles \(ABH\), \(BCH\), and \(ACH\) respectively.

The set of symmetries of an object (e.g. a square) form an object called a group. We can formally define a group \(G\) as follows.

A is a non-empty set \(G\) with a binary operation \(*\) satisfying the following axioms (you can think of them as rules). A binary operation takes two elements of \(G\) and gives another element of \(G\).

1. Closure: For all \(g\) and \(h\) in \(G\), \(g*h\) is also in \(G\).

2. Identity: There is an element \(e\) of \(G\) such that \(e*g=g=g*e\) for all \(g\) in \(G\).

3. Associativity: For all \(g\), \(h\) and \(k\) in \(G\), \((g*h)*k=g*(h*k)\).

4. Inverses: For every \(g\) in \(G\), there exists a \(g^{-1}\) in \(G\) such that \(g*g^{-1}=e\).

Prove that the symmetries of the ‘reduce-reuse-recycle’ symbol form a group.