Problems

Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Consider the Euler circle of the triangle \(ABC\), the one that contains the points \(D,J,I,E,F,K\). This circle intersects the segments \(AH\), \(BH\), \(CH\) at points \(O\), \(P\), \(Q\) respectively. Prove that \(O\), \(P\), \(Q\) are the midpoints of the segments \(AH\), \(BH\), \(CH\).

Consider the point \(H\) of intersection of the heights of the triangle \(ABC\). Prove that Euler lines of the triangles \(ABC\), \(ABH\), \(BCH\), \(ACH\) intersect at one point. On the diagram below the points \(R,S,T\) are the points of intersection of medians in triangles \(ABH\), \(BCH\), and \(ACH\) correspondingly.

The set of symmetries of an object (e.g. a square) form an object called a group. We can formally define a group \(G\) as follows.

A is a non-empty set \(G\) with a binary operation \(*\) satisfying the following axioms (you can think of them as rules). A binary operation takes two elements of \(G\) and gives another element of \(G\).

1. Closure: For all \(g\) and \(h\) in \(G\), \(g*h\) is also in \(G\).

2. Identity: There is an element \(e\) of \(G\) such that \(e*g=g=g*e\) for all \(g\) in \(G\).

3. Associativity: For all \(g\), \(h\) and \(k\) in \(G\), \((g*h)*k=g*(h*k)\).

4. Inverses: For every \(g\) in \(G\), there exists a \(g^{-1}\) in \(G\) such that \(g*g^{-1}=e\).

Prove that the symmetries of the ‘reduce-reuse-recycle’ symbol form a group.

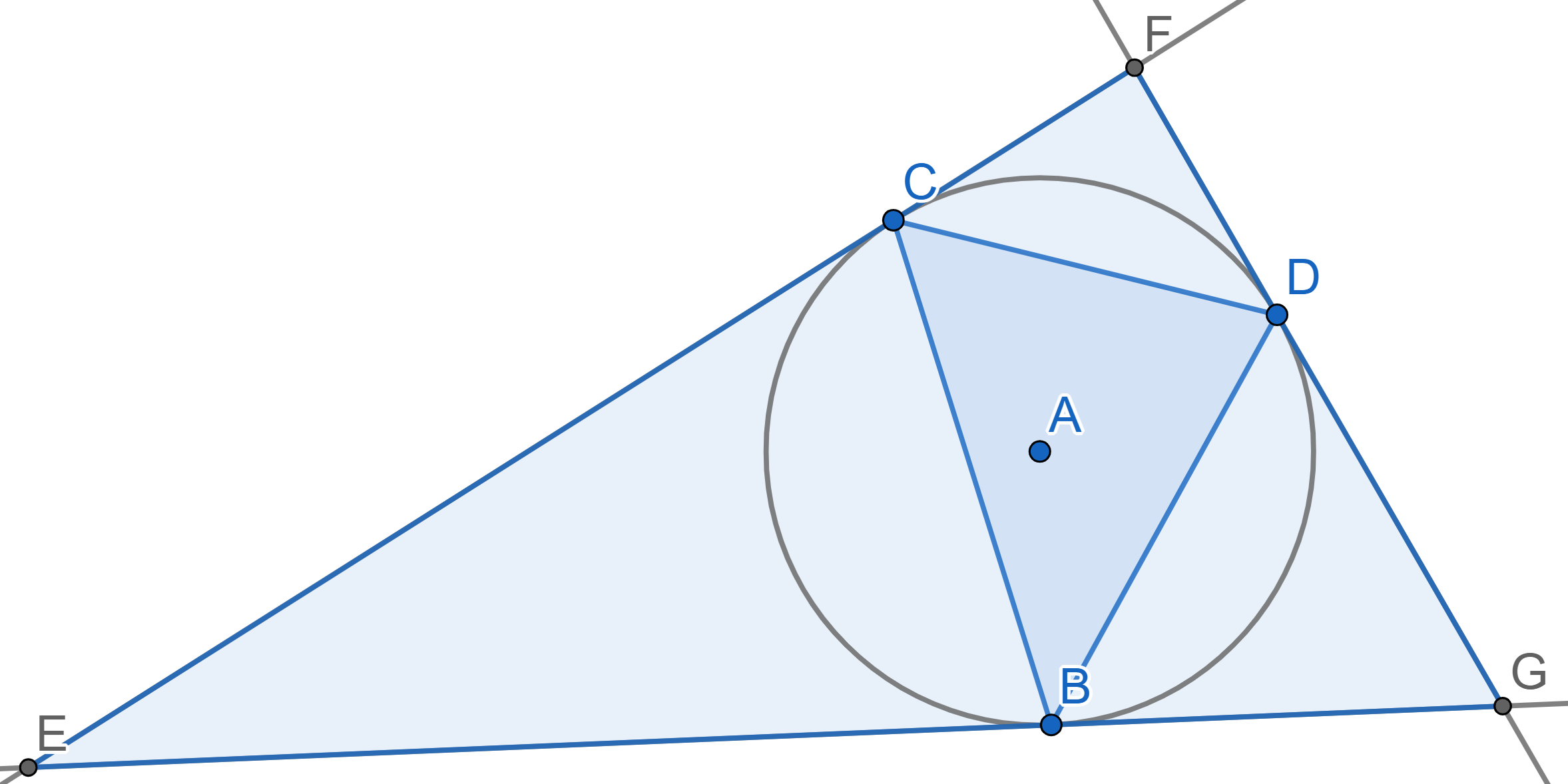
Consider the triangle \(BCD\), inscribed in a circle with center \(A\), the segments \(EF\), \(FG\), \(EG\) are tangent to the circle at the points \(C\), \(D\), \(B\) respectively. Prove that the Euler line of the triangle \(BCD\) passes through the center of the circle circumscribed around the triangle \(EFG\).

Find all positive integers \((x,n)\) such that \(x^n + 2^n + 1\) is a divisor \(x^{n+1} + 2^{n+1} + 1\).

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

Let \(X\) be a finite set, and let \(\mathcal{P}X\) be the power set of \(X\) - that is, the set of subsets of \(X\). For subsets \(A\) and \(B\) of \(X\), define \(A*B\) as the symmetric difference of \(A\) and \(B\) - that is, those elements that are in either \(A\) or \(B\), but not both. In formal set theory notation, this is \(A*B=(A\cup B)\backslash(A\cap B)\).

Prove that \((\mathcal{P}X,*)\) forms a group.

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

You have a row of coins and you can perform these three operations as many times as you like:

1. Remove three adjacent heads

2. Remove two adjacent tails

3. If there’s a tail followed by a heads, then turn the tail over and put a new tail after both heads

You apply these operations until you can’t make any more moves. Show that you will always get the same configuration at the end, no matter the order.