We solve problems

Problem #PRU-100112

Problems Algebra and arithmetic Arithmetics. Mental maths Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

10–10

Replace the letters with digits in a way that makes the following sum as big as possible: \[SEND +MORE +MONEY.\]

Problem #PRU-100113

Problems Algebra and arithmetic Arithmetics. Mental maths Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

Jane wrote another number on the board. This time it was a two-digit number and again it did not include digit 5. Jane then decided to include it, but the number was written too close to the edge, so she decided to t the 5 in between the two digits. She noticed that the resulting number is 11 times larger than the original. What is the sum of digits of the new number?

Problem #PRU-100114

Problems Algebra and arithmetic Arithmetics. Mental maths Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

a) Find the biggest 6-digit integer number such that each digit, except for the two on the left, is equal to the sum of its two left neighbours.

b) Find the biggest integer number such that each digit, except for the rst two, is equal to the sum of its two left neighbours. (Compared to part (a), we removed the 6-digit number restriction.)

Problem #PRU-100202

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?

Problem #PRU-100203

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.

Problem #PRU-100204

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

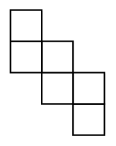
Tile the whole plane with the following shapes:

Problem #PRU-100205

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

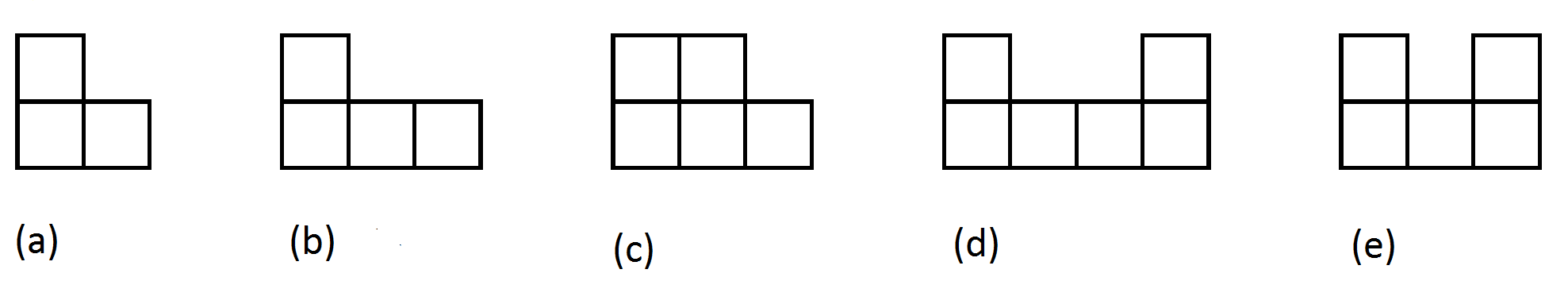
David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrosae looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

Problem #PRU-100206

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

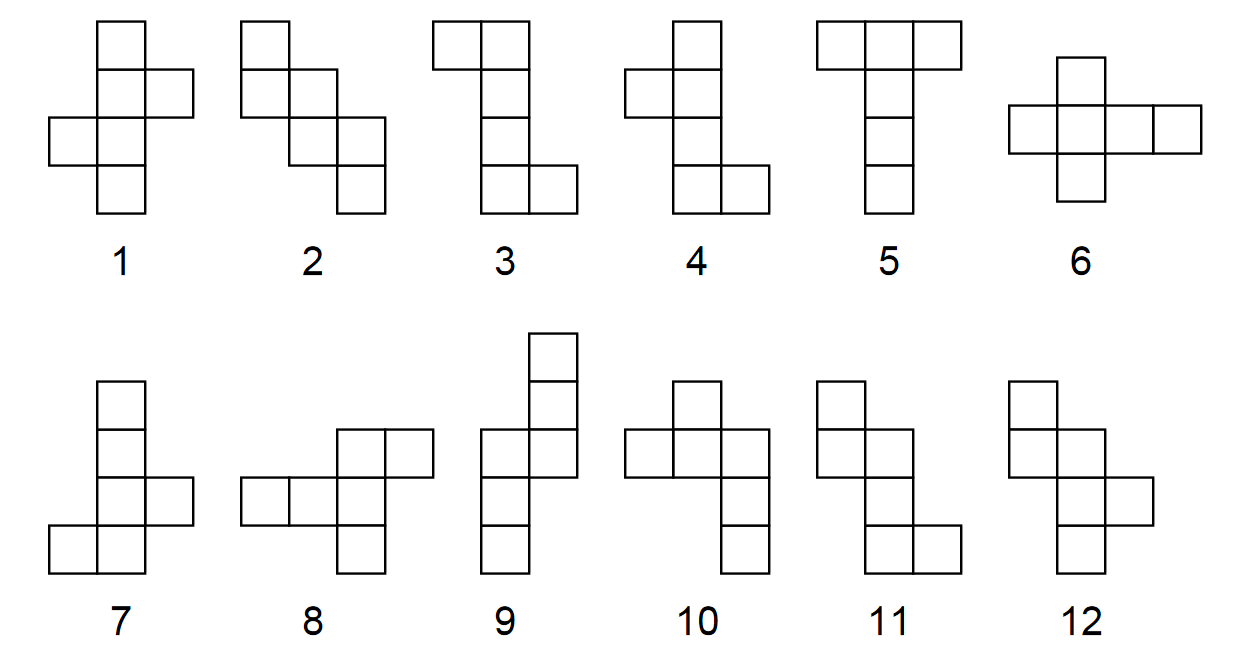
It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with nets below:

Problem #PRU-100213

Problems Geometry Plane geometry Locus Locus and auxiliary triangles

Think of other shapes Robinson’s goat can graze without a wolf, or with a wolf tied nearby. What if Robinson managed to tame several wolves and used them as guard dogs? Can two tied wolves keep an untied goat in a triangle? Can you think of other shapes you can create with Robinson’s goat and wolves?

Problem #PRU-100216

Problems Number Theory Divisibility Divisibility of a number. General properties

While studying numbers and its properites, Robinson came across a 3-digit prime number with the last digit being equal to the sum of the first two digits. What was the last digit of that number if among the number did not have any zeros among it’s digits?