Problems

Let’s call a natural number good if in its decimal record we have the numbers 1, 9, 7, 3 in succession, and bad if otherwise. (For example, the number 197,639,917 is bad and the number 116,519,732 is good.) Prove that there exists a positive integer \(n\) such that among all \(n\)-digit numbers (from \(10^{n-1}\) to \(10^{n-1}\)) there are more good than bad numbers.

Try to find the smallest possible \(n\).

Find the minimum for all \(\alpha\), \(\beta\) of the maximum of the function \(y (x) = | \cos x + \alpha \cos 2x + \beta \cos 3x |\).

We consider a sequence of words consisting of the letters “A” and “B”. The first word in the sequence is “A”, the \(k\)-th word is obtained from the \((k-1)\)-th by the following operation: each “A” is replaced by “AAB” and each “B” by “A”. It is easy to see that each word is the beginning of the next, thus obtaining an infinite sequence of letters: AABAABAAABAABAAAB...

a) Where in this sequence will the 1000th letter “A” be?

b) Prove that this sequence is non-periodic.

In the Land of Linguists live \(m\) people, who have opportunity to speak \(n\) languages. Each person knows exactly three languages, and the sets of known languages may be different for different people. It is known that \(k\) is the maximum number of people, any two of whom can talk without interpreters. It turned out that \(11n \leq k \leq m/2\). Prove that then there are at least \(mn\) pairs of people in the country who will not be able to talk without interpreters.

Hard. Let \(\mathcal{S}\) be a finite set of at least two points in the plane. Assume that no three points of \(\mathcal S\) are collinear. A windmill is a process that starts with a line \(\ell\) going through a single point \(P \in \mathcal S\). The line rotates clockwise about the pivot \(P\) until the first time that the line meets some other point belonging to \(\mathcal S\). This point, \(Q\), takes over as the new pivot, and the line now rotates clockwise about \(Q\), until it next meets a point of \(\mathcal S\). This process continues indefinitely. Show that we can choose a point \(P\) in \(\mathcal S\) and a line \(\ell\) going through \(P\) such that the resulting windmill uses each point of \(\mathcal S\) as a pivot infinitely many times.

The king decided to reward a group of \(n\) wise men. They will be placed in a row one after the other (so that everyone is looking in the same direction), and each is going to wear a black or a white hat. Everyone will see the hats of everyone in front, but not those behind them. The wise men will take turns (from the last to the first) to name the color (white or black) and the natural number of their choice.
At the end, the number of sages who have named the color of their hat correctly is counted: that is exactly how many days the whole group will be paid a salary raise. The wise men were allowed to agree in advance on how to respond. At the same time, the wise men know that exactly \(k\) of them are insane (they do not know who exactly). Any insane man names the color white or black, regardless of the agreement. What is the maximum number of days with a pay supplement that the wise men can guarantee to a group, regardless of the location of the insane in the queue?

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

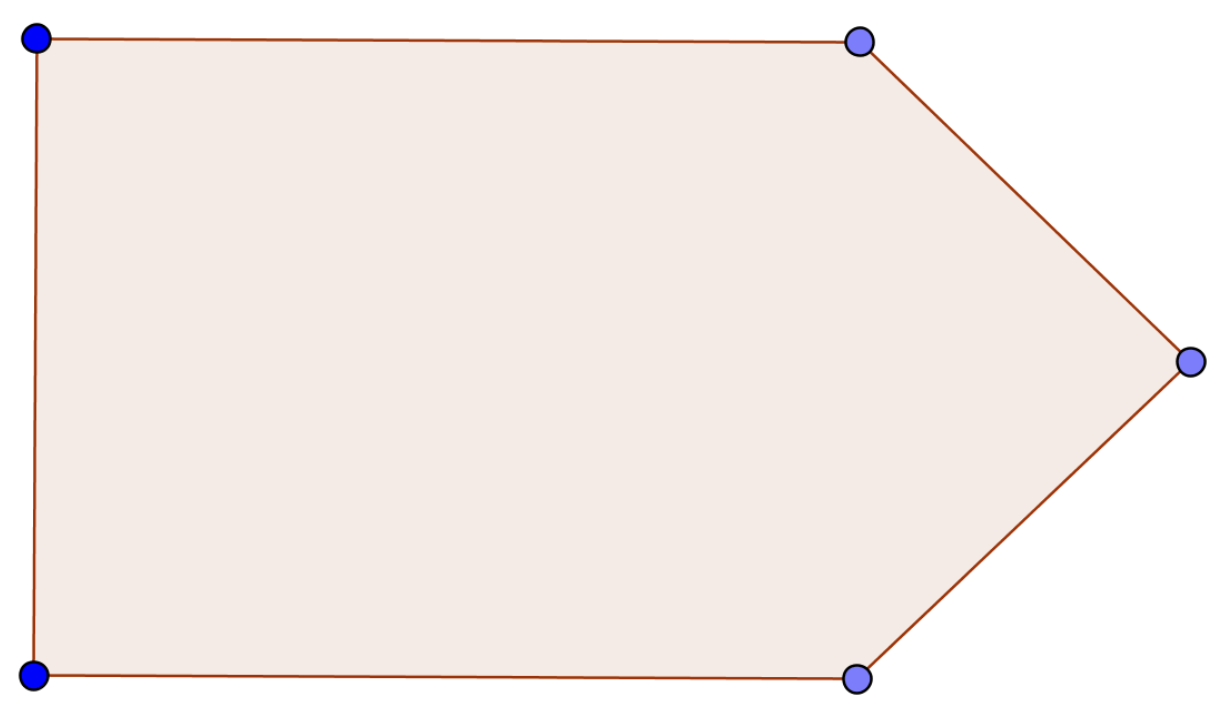
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.