Problems

What’s \(\sum_{i=0}^nF_i^2=F_0^2+F_1^2+F_2^2+...+F_{n-1}^2+F_n^2\) in terms of just \(F_n\) and \(F_{n+1}\)?

What are the ratios \(\frac{F_2}{F_1}\), \(\frac{F_3}{F_2}\), and so on until \(\frac{F_7}{F_6}\)? What do you notice about them?

\(\varphi=\frac{1+\sqrt{5}}{2}\) is the golden ratio. Using the fact that \(\varphi^2=\varphi+1\), can you express \(\varphi^3\) in the form \(a\varphi+b\), where \(a\) and \(b\) are positive integers?

Let \(m\) and \(n\) be positive integers. What positive integers can be written as \(m+n+\gcd(m,n)+\text{lcm}(m,n)\), for some \(m\) and \(n\)?

Let \(n\ge r\) be positive integers. What is \(F_n^2-F_{n-r}F_{n+r}\) in terms of \(F_r\)?

On the questioners’ planet (where everyone can only ask questions. Cricks can only ask questions to which the answer is yes, and Goops can only ask questions to which the answer is no), you meet 4 alien mathematicians.

They’re called Alexander Grothendieck, Bernhard Riemann, Claire Voisin and Daniel Kan (you may like to shorten their names to \(A\), \(B\), \(C\) and \(D\)).
Alexander asks the following question “Am I the kind who could ask whether Bernhard could ask whether Claire could ask whether Daniel is a Goop?"

Amongst the final three (that is, Bernhard, Claire and Daniel), are there an even or an odd number of Goops?

On the questioners’ planet, there are two types of aliens, Cricks and Goops. These aliens can only ask questions. Cricks can only ask questions to which the answer is yes, Goops can only ask questions to which the answer is no.

There are 19 aliens standing in a circle. Each of them asks the following question “Do I have a Crick standing next to me on both sides?" Then one of them asks you in private “Is 57 a prime number?" How many Cricks were actually in the circle?

Suppose that \(n\) is a natural number and \(p\) is a prime number. How many numbers are there less than \(p^n\) that are relatively prime to \(p^n\)?

In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.

This is a closed knight’s tour on a \(6\times6\) chessboard.

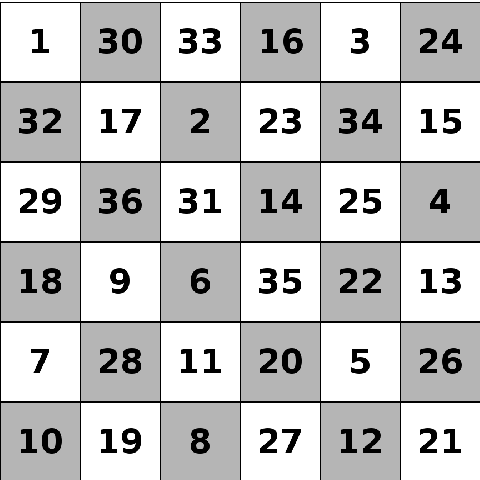
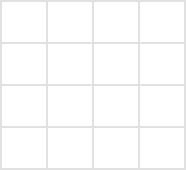
Can you draw a closed knight’s tour on a \(4\times4\) torus? That is, a \(4\times4\) square with both pairs of opposite sides identified in the same direction, like the diagram below.

Prove that one can tile the whole plane without spaces and overlaps, using any non self-intersecting quadrilaterals of the same shape. Note: quadrilaterals might not be convex.