Problems

A whole number of litres of water were poured into three vessels. You can only to pour into any vessel the exact amount of water equal to the amount it already contains from any other vessel. Prove that in a few transfusions one can empty one of the vessels. The vessels are large enough: each can hold all the water.

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

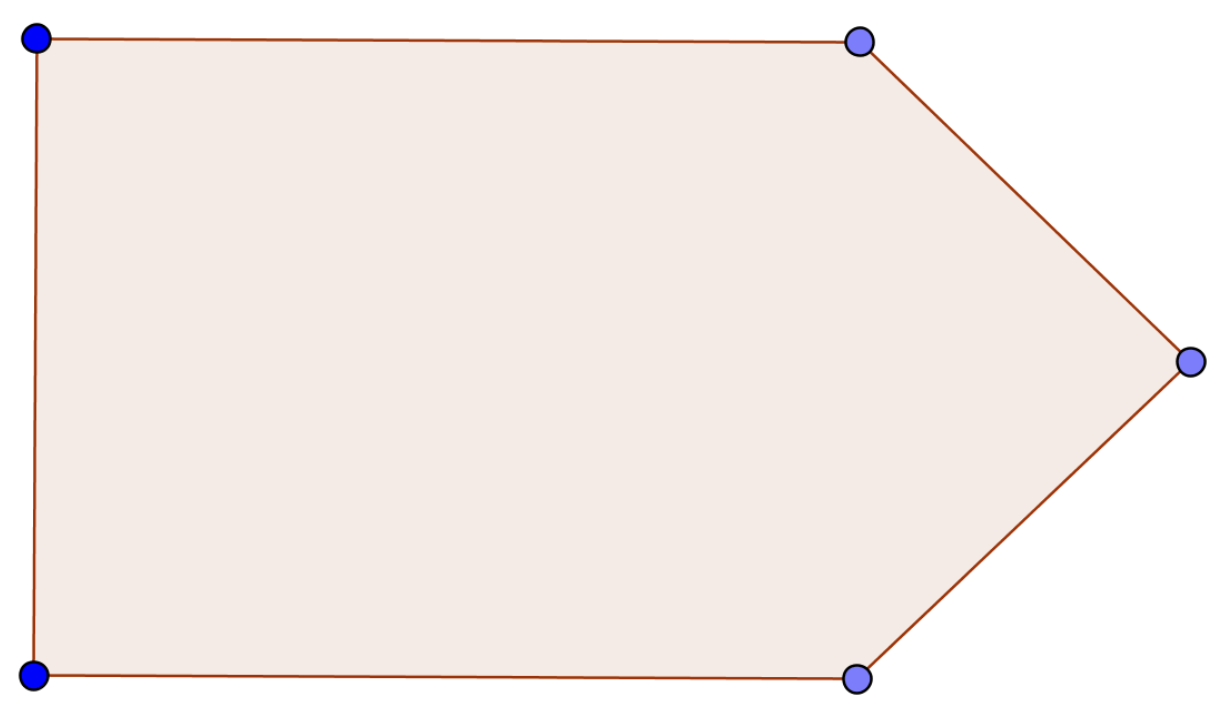
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.

On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?

Split the numbers from \(1\) to \(9\) into three triplets such that the sum of the three numbers in each triplet is prime. For example, if you split them into \(124\), \(356\) and \(789\), then the triplet \(124\) is correct, since \(1+2+4=7\) is prime. But the other two triples are incorrect, since \(3+5+6=14\) and \(7+8+9=24\) are not prime.

A family is going on a big holiday, visiting Austria, Bulgaria, Cyprus, Denmark and Estonia. They want to go to Estonia before Bulgaria. How many ways can they visit the five countries, subject to this constraint?

Let \(p\), \(q\) and \(r\) be distinct primes at least \(5\). Can \(p^2+q^2+r^2\) be prime? If yes, then give an example. If no, then prove it.

How many subsets of \(\{1,2,...,n\}\) (that is, the integers from \(1\) to \(n\)) have an even product? For the purposes of this question, take the product of the numbers in the empty set to be \(1\).