Problems
Let \(p\), \(q\) and \(r\) be distinct primes at least \(5\). Can \(p^2+q^2+r^2\) be prime? If yes, then give an example. If no, then prove it.
How many subsets of \(\{1,2,...,n\}\) (that is, the integers from \(1\) to \(n\)) have an even product? For the purposes of this question, take the product of the numbers in the empty set to be \(1\).
How many subsets are there of \(\{1,2,...,n\}\) (the integers from \(1\) to \(n\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these
Let \(A\), \(B\), \(C\) and \(D\) be four points labelled clockwise on the circumference of a circle. The diagonals \(AC\) and \(BD\) intersect at the centre \(O\) of the circle. What can be deduced about the quadrilateral \(ABCD\)?
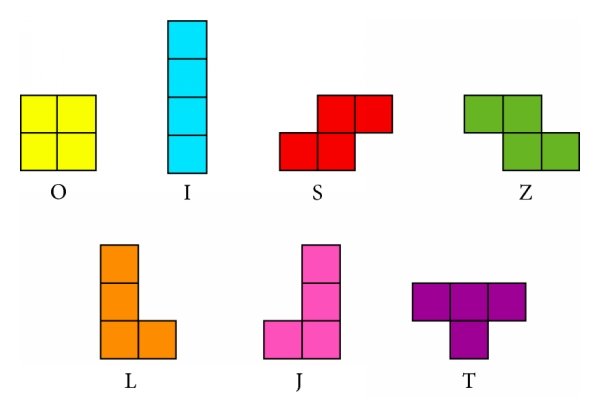
Consider the 7 different tetrominoes. Is it possible to cover a \(4\times7\) rectangle with exactly one copy of each of the tetrominoes? If it is possible, provide an example layout. If it is not possible, prove that it’s impossible.
We allow rotation of the tetrominoes, but not reflection. This means that we consider \(S\) and \(Z\) as different, as well as \(L\) and \(J\).
In the following grid, how many different ways are there of getting from the bottom left triangle to the bottom right triangle? You must only go from between triangles that share an edge and you can visit each triangle at most once. (You don’t have to visit all of the triangles.)
I have three positive integers. When you add them together, you get \(15\). When you multiply the three numbers together, you get \(120\).
What are the three numbers?
Is there a divisibility rule for \(2^n\), where \(n = 1\), \(2\), \(3\), . . .? If so, then explain why the rule works.
Can you find a formula relating \(1^3+2^3+\dots+n^3\) to \(1+2+\dots+n\)?