Problems

One three-digit number consists of different digits that are in ascending order, and in its name all words begin with the same letter. The other three-digit number, on the contrary, consists of identical digits, but in its name all words begin with different letters. What are these numbers?

Replace the question marks with the appropriate letters or words:

a) r, o, y, g, b, ?, ?;

b) a, c, f, j, ?, ?;

c) one, three, five, ?,

d) A, H, I, M, O, T, U, ?, ?, ?, ?;

e) o, t, t, f, f, s, s, e, ?, ?.

A traveller rents a room in an inn for a week and offers the innkeeper a chain of seven silver links as payment – one link per day, with the condition that they will be payed everyday. The innkeeper agrees, with the condition that the traveller can only cut one of the links. How did the traveller manage to pay the innkeeper?

There are five chain links with 3 rings in each. What is the smallest number of rings that need to be unhooked and hooked together to connect these links into one chain?

During a chess tournament, some of the players played an odd number of games. Prove that the number of such players is even.

In an apartment building in which there are only married couples with children, a population census was carried out. The person who conducted the census stated in the report: “There are more adults in the building than children. Each boy has a sister and there are more boys than girls. There are no childless families.” This report was incorrect. Why?

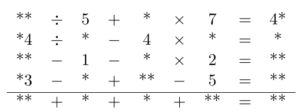
In the rebus in the diagram below, the arithmetic operations are carried out from left to right (even though the brackets are not written).

For example, in the first row "\(** \div 5 + * \times 7 = 4*\)" is the same as "\(((** \div 5) +*) \times 7 = 4*\)". Each number in the last row is the sum of the numbers in the column above it. The result of each \(n\)-th row is equal to the sum of the first four numbers in the \(n\)-th column. All of the numbers in this rebus are non-zero and do not begin with a zero, however they could end with a zero. That is, 10 is allowed but not 01 or 0. Solve the rebus.

There are scales without weights and 3 identical in appearance coins, one of which is fake: it is lighter than the real ones (the real coins are of the same weight). How many weightings are needed to determine the counterfeit coin? Solve the same problem in the cases where there are 4 coins and 9 coins.

We have scales without weights and 3 identical in appearance coins. One of the coins is fake, and it is not known whether it is lighter or heavier than the real coins (note that all real coins are of the same weight). How many weighings are needed to determine the counterfeit coin? Solve the same problem in the cases where there are 4 coins and 9 coins.

Decode this rebus: replace the asterisks with numbers such that the equalities in each row are true and such that each number in the bottom row is equal to the sum of the numbers in the column above it.