Problems
Denote by \(GCD(m,n)\) the greatest common divisor of numbers \(m,n\), namely the largest possible \(d\) which divides both \(n\) and \(m\). Prove for any \(m,n\) that \[GCD(F_n,F_m) = F_{GCD(m,n)}.\]
Suppose that \(p\) is a prime number. How many numbers are there less than \(p^2\) that are relatively prime to \(p^2\)?
How many cuboids are contained in an \(n\times n\times n\) cube? For example, we’ve got \(n^3\) cuboids of size \(1\times1\times1\), and obviously just \(1\) of size \(n\times n\times n\) (which is the whole cube itself). But we also have to count how many there of size \(1\times1\times2\), \(1\times2\times3\), and several more.
In the \(6\times7\) large rectangle shown below, how many rectangles are there in total formed by grid lines? [need to insert image]
Simplify \(F_0-F_1+F_2-F_3+...-F_{2n-1}+F_{2n}\), where \(n\) is a positive integer.
Explain why a position \(g\) is a winning position if there is a move that turns \(g\) into a losing position. On the other hand, explain why a position is a losing position if all moves turns it into a winning position.
A technique that can be used to completely solve certain games is drawing game graphs. Given a game \(G\), we draw an arrow pointing from a position \(g\) to a position \(h\) if there is a move from \(g\) to \(h\).
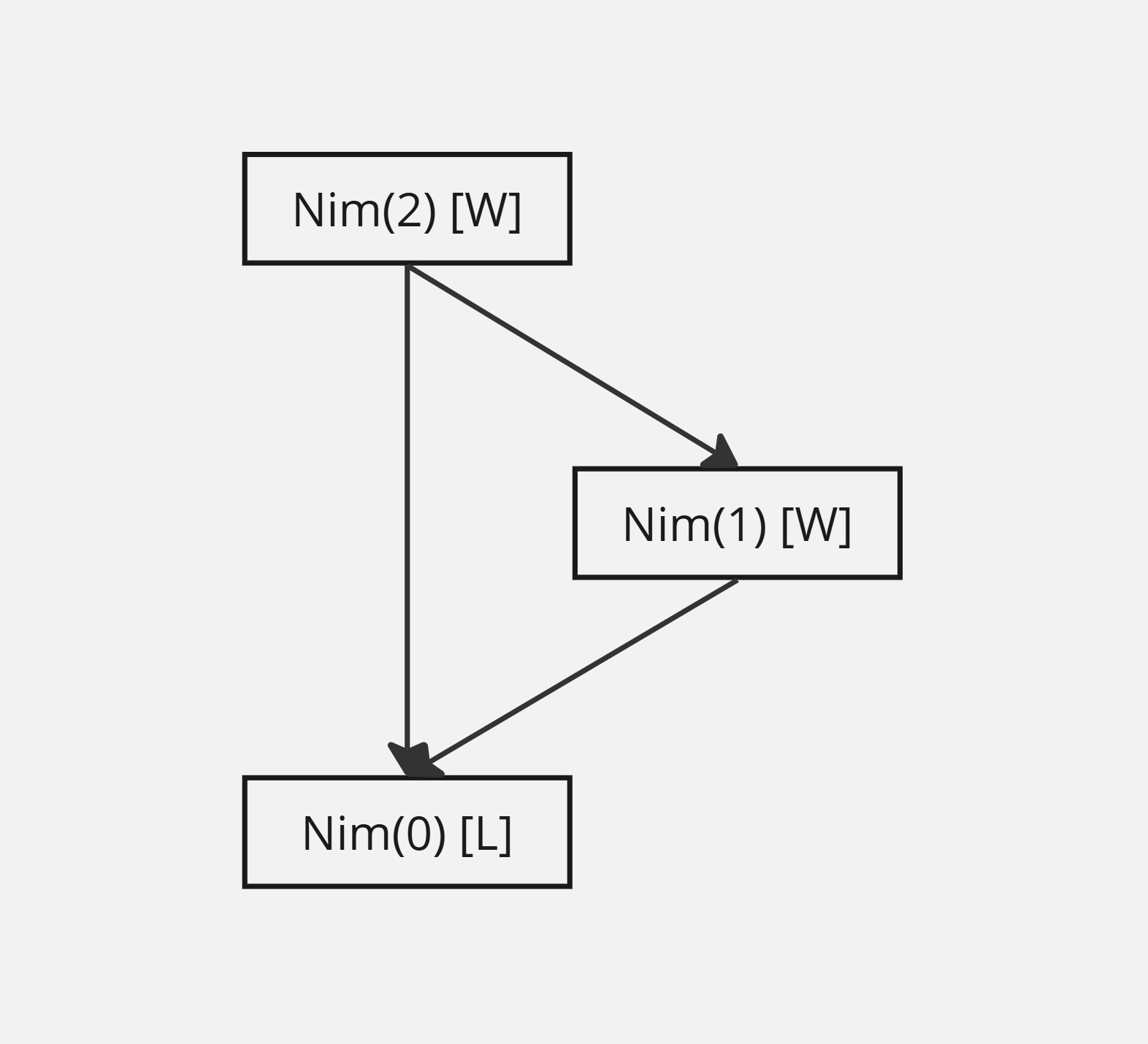
As a simple example, the game graph of \(\text{Nim}(2)\) is shown below.
Draw the game graph of \(\text{Nim}(2,2)\). Is \(\text{Nim}(2,2)\) a winning position or losing position?
Let \(x,y\) be nonnegative integers. Determine when \(\text{Nim}(x,y)\) is a losing position and when it is a winning position.