Problems
The kingdom of Triangland is an equilateral triangle of side \(10\) km. There are \(5\) cities in this kingdom. Show that some two of them are closer than \(5\) km apart.
Margaret marked three points with integer coordinates on a number line with a red crayon. Meanwhile Angelina marked the midpoint of each pair of red points with a blue crayon. Prove that at least one of the blue points has an integer coordinate.
Margaret and Angelina coloured points in the second dimension. Now Margaret marked five points with both integer coordinates on a plane with a red crayon, while Angelina marked the midpoint for each pair of red points with a blue crayon. Prove that at least one of the blue points has both integer coordinates.
Anna has a garden of square shape with side \(4\) m. After playing with her dog in the garden she left \(5\) dog toys on the lawn. Show that some two of them are closer than \(3\) m apart.
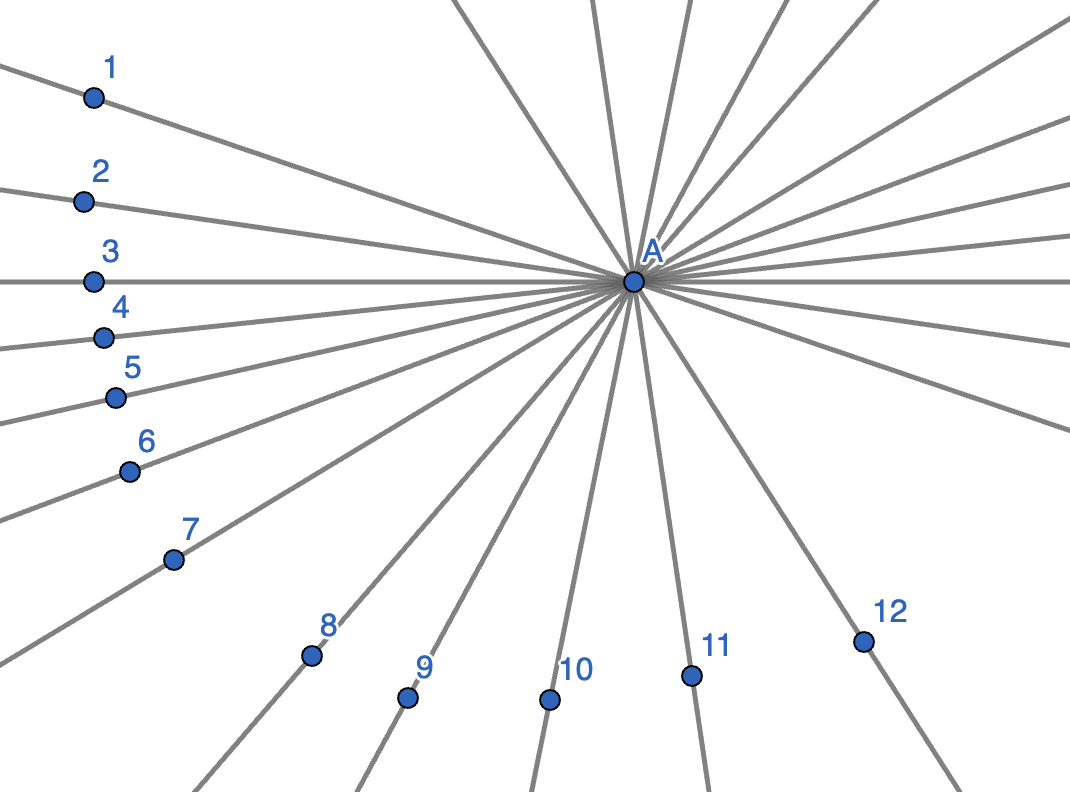
Twelve lines are drawn on the plane, passing through a point \(A\). Prove that there are two of them with angle less than \(17^{\circ}\) between them.
Inside a square of area \(6\), there are three polygons, each of area \(3\). Show that some two of these polygons overlap and the area of the overlap is at least \(1\).
A Wimbledon doubles court is \(78\)ft\(\times36\)ft. After a long practice match, there were \(79\) tennis balls in the court area. Show that some two of the balls were at most \(6\sqrt{2}\)ft away from each other.
There are \(n\) ambassadors, each from a different country, sitting at a round table. The flag for each country is on the table, but unfortunately the flags have been mixed up. As a result each ambassador has a wrong flag in front of them, while their flag is in front of some other ambassador. Show that you can rotate the table with the flags on it, in such a way that at least two ambassadors will have correct flags in front of them.
We have an infinitely large chessboard, consisting of white and black squares. We would like to place a stain of a specific shape on this chessboard. The stain is a bounded and connected shape with an area strictly less than the area of one square of the chessboard. Show that it is always possible to place the stain in such a way that it does not cover a vertex of any square.
There are \(n\) straight lines on a plane, no two among them are parallel to each other. Show that some two of them cross at an angle no more than \(\frac{180^{\circ}}{n}\).