Problems
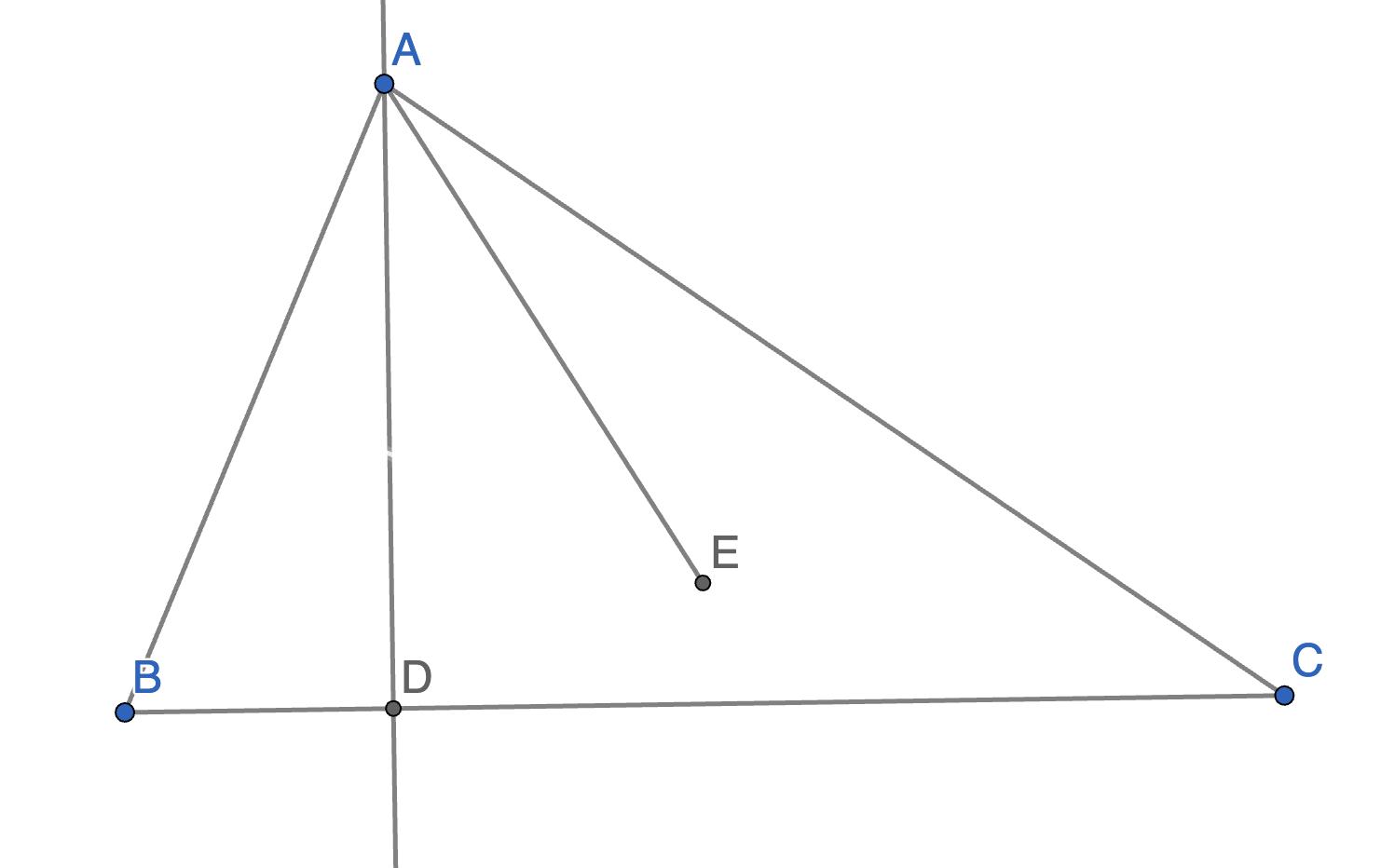
The triangle \(ABC\) is inscribed into the circle with centre \(E\), the line \(AD\) is perpendicular to \(BC\). Prove that the angles \(\angle BAD\) and \(\angle CAE\) are equal.
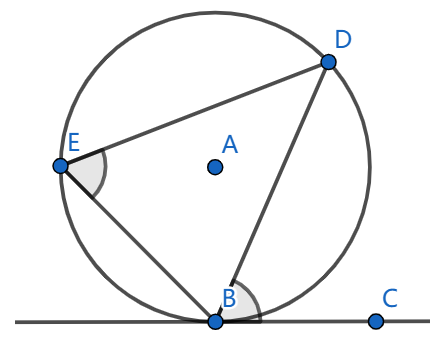
On the diagram below \(BC\) is the tangent line to a circle with the centre \(A\), and it is known that the angle \(\angle ABC = 90^{\circ}\). Prove that the angles \(\angle DEB\) and \(\angle DBC\) are equal.
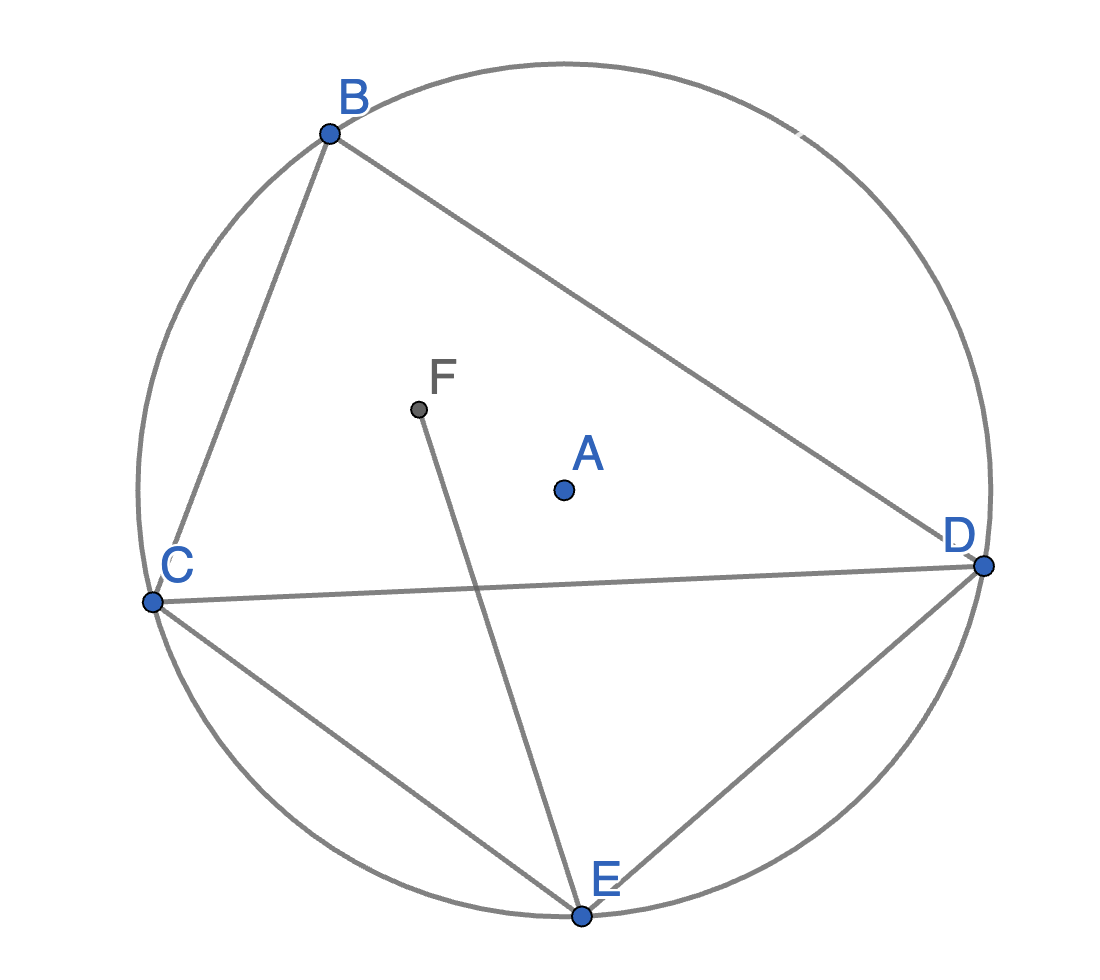
The triangle \(BCD\) is inscribed in a circle with the centre \(A\). The point \(E\) is chosen as the midpoint of the arc \(CD\) which does not contain \(B\), the point \(F\) is the centre of the circle inscribed into \(BCD\). Prove that \(EC = EF = ED\).
Picasso got a new set of crayons. He started colouring various things. First, Picasso coloured a line under the following condition: each point on a line is coloured either red or blue. Show that there are three different points \(A,B,C\) on the line of the same colour such that \(AB = BC\).
Monet has coloured a plane. He wants to colour the entire plane in such a way that each straight line can only have points of three or fewer different colours. Show that he can use however many different colours he wants and still be able to achieve this goal.
Frida colours the plane. She decided to use \(9\) different colours, but she wants to colour the entire infinite plane in such a way that if two points are distance \(1\) apart, then they must be different colours. Show that this is always possible.
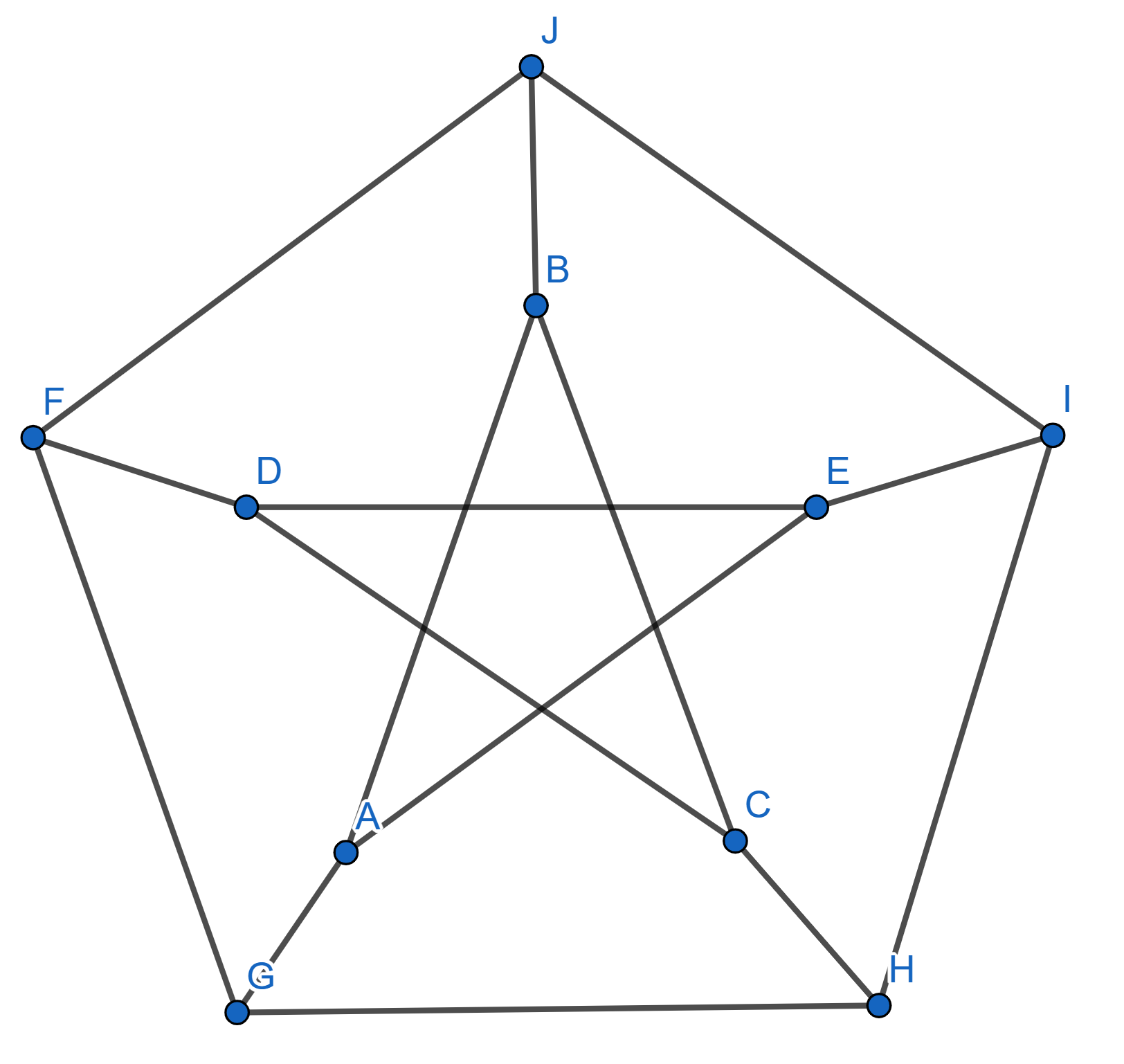
Mondrian coloured the vertices of a regular pentagon. He used only red and blue. Show that there are three vertices of the pentagon which are all the same colour and form an isosceles triangle.
Artemisia coloured the plane with red and blue crayons. Show that there is an equilateral triangle with all vertices of the same colour somewhere on the plane.
Andy used two colours to colour the plane, red and green. Show that there is a segment of length \(1\) whose endpoints are the same colour.
Find the minimum number of colours Raphael needs to paint the following figure in such a way that no connected points are of the same colour.