Problems
Picasso colours every point on the circumference of a circle red or blue. Is he guaranteed to create an equilateral triangle all of whose vertices are the same colour?
Let \(A\), \(B\), \(C\), \(D\), \(E\) be five different points on the circumference of a circle in that (cyclic) order. Let \(F\) be the intersection of chords \(BD\) and \(CE\). Show that if \(AB=AE=AF\) then lines \(AF\) and \(CD\) are perpendicular.
Let \(a\), \(b\) and \(c\) be positive real numbers such that \(a+b+c=3\). Prove that \(a^a+b^b+c^c\ge3\).
David and Esther play the following game. Initially, there are three piles, each containing 1000 stones. The players take turns to make a move, with David going first. Each move consists of choosing one of the piles available, removing the unchosen pile(s) from the game, and then dividing the chosen pile into 2 or 3 non-empty piles. A player loses the game if they are unable to make a move. Prove that Esther can always win the game, no matter how David plays.
Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.
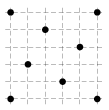
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.
The Tour de Clochemerle is not yet as big as the rival Tour de France. This year there were five riders, Arouet, Barthes, Camus, Diderot and Eluard, who took part in five stages. The winner of each stage got \(5\) points, the runner up \(4\) points and so on down to the last rider who got \(1\) point. The total number of points acquired over the five states was the rider’s score. Each rider obtained a different score overall and the riders finished the whole tour in alphabetical order with Arouet gaining a magnificent 24 points. Camus showed consistency by gaining the same position in four of the five stages and Eluard’s rather dismal performance was relieved by a third place in the fourth stage and first place in the final stage.
Where did Barthes come in the final stage?
As the title suggests, today we’re going to colour some (if not all!) points in the plane, using only a couple of colours. We’ll show that no matter how we do this colouring, we’re guaranteed to get some structure. When we say ‘the plane’, imagine a flat piece of paper extending infinitely far in every direction.
Let’s look at some examples!
Certain geometric objects nicely blend when they happen to be
together in a problem. One possible example of such a pair of objects is
a circle and an inscribed angle.
We will be using the following statements in the examples and
problems:
1. The supplementary angles (angles “hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
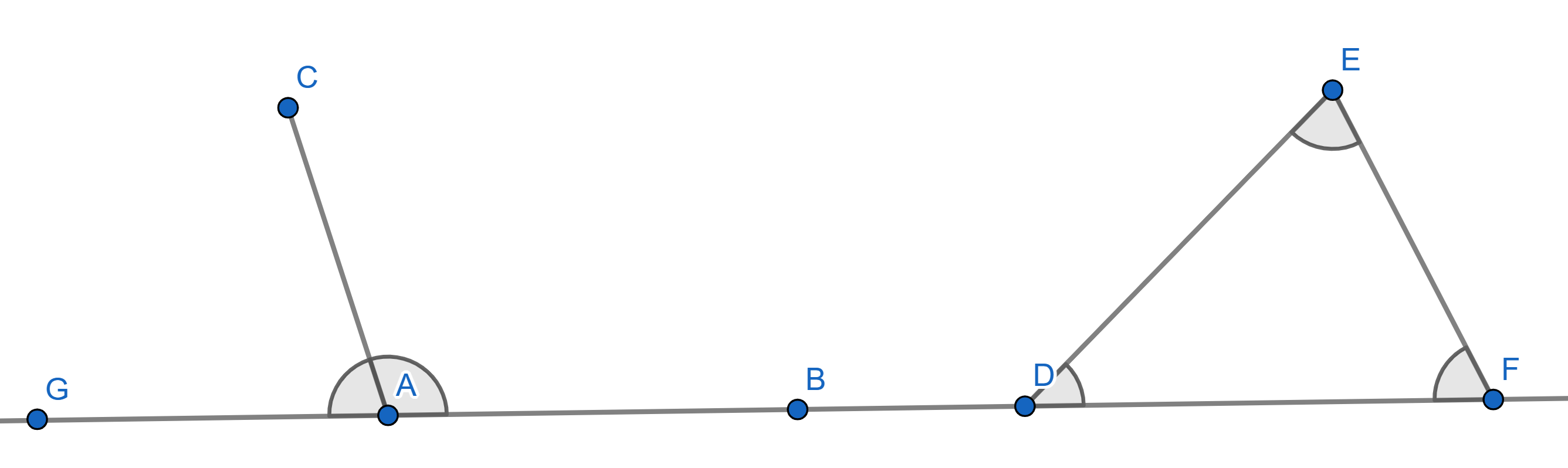
3. Two triangles are said to be “congruent" if ALL of their
corresponding sides and angles are equal.
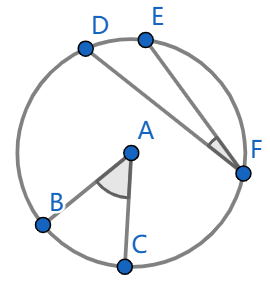
The following terminology will also be quite helpful. In the picture
below, the points \(B\) and \(C\) lie on the circumference of the circle
while the vertex \(A\) lies at the
centre of the circle. We say that the angle \(\angle BAC\) is a central angle.
The angle \(\angle DFE\) is called an
inscribed angle because the vertices \(D\), \(F\)
and \(E\) all lie on the circumference
of the circle.
Prove that the product of five consecutive integers is divisible by \(120\).