Problems

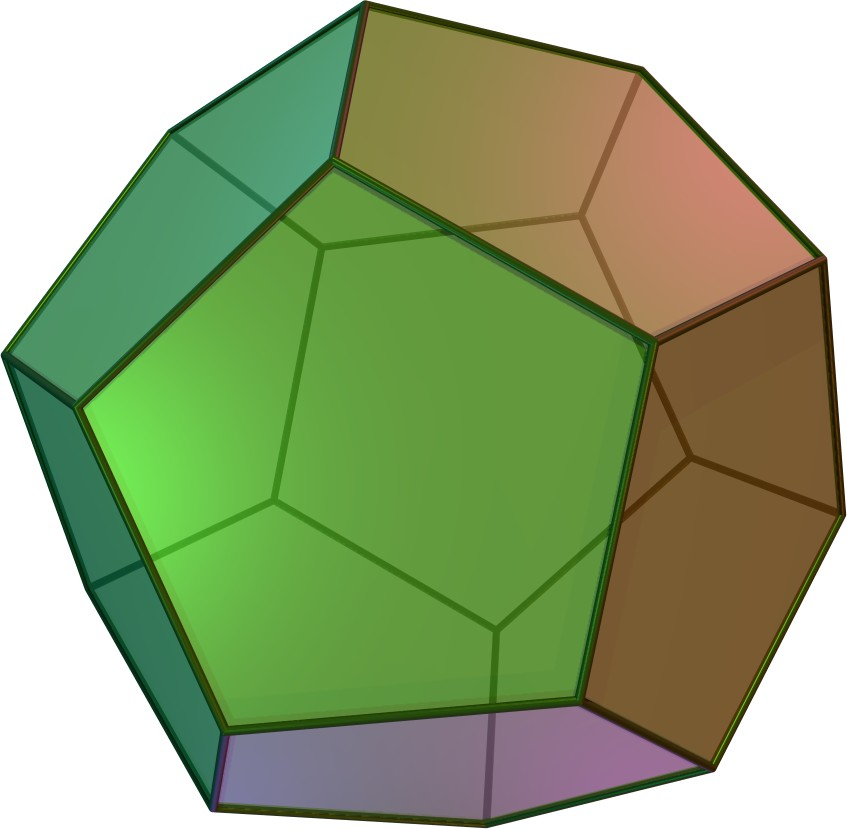
Take a regular dodecahedron as in the image. It has \(12\) regular pentagons as its faces, \(30\) edges, and \(20\) vertices. We can cut it with planes in various ways and the cut will be a polygon on a plane. Find out how many ways there are to cut a dodecahedron with a plane so that the polygon obtained is a regular hexagon.

For an odd number \(N\) denote by \(A\) the minimal positive difference between prime divisors of \(N\), denote by \(B\) the minimal positive difference between composite divisors of \(N\). Usually we have \(A<B\), but can we have \(A>B\)? (Disregard numbers such as \(15\) where one of \(A\) or \(B\) is not defined)

Let \(n\) be an integer bigger than \(1\), and \(p\) a prime number. Suppose that \(n\) divides \(p-1\) and \(p\) divides \(n^3-1\). Prove that \(4p-3\) is a square number.

Let \(n\) be a composite number. Arrange the factors of \(n\) greater than \(1\) in a circle. When can this be done such that neighbours in the circle are never coprime?

Let \(x\), \(y\), \(z\) and \(w\) be non-negative integers. Find all solutions to \(2^x3^y-5^z7^w=1\).

A natural number \(N\) is called perfect if it equals the sum of its divisors, except for \(N\) itself. Prove that if \(2^r-1\) is prime, then \((2^r-1)2^{r-1}\) is a perfect number. Are there any odd perfect numbers?

A robot is programmed to move along the number line starting at \(2\). At each second, the number by which it moves up by must be a factor of the number it’s currently on, but not \(1\). For example, if the robot gets to \(10\), then it can move forward by \(2\), \(5\) or \(10\) steps, going to \(12\), \(15\), or \(20\). What numbers can it land on, and what numbers can’t it land on?

A gang of three jewel thieves has stolen some gold coins and wants to divide them fairly. However, they each have one unusual rule: (i) The first thief wants the number of coins to be divisible by \(3\) so they can split it evenly. (ii) The second thief wants the number of coins to be divisible by \(5\) because she wants to split her share with her four siblings. (iii) The third thief wants the number of coins to be divisible by \(7\) since he wants to split his share amongst seven company stocks.

However, they’re stuck as the number of coins isn’t divisible by any of these numbers. In fact, the number of coins is \(1\) more than a multiple of \(3\), \(3\) more than a multiple of \(5\) and \(5\) more than a multiple of \(7\).
What’s the smallest number of coins they could have? (And if you’re feeling generous, how would you help them out?)

Munira wants to put \(6\) books on her shelf, \(4\) of which are red and \(2\) of which are blue. The four red ones are a small paperback, a small hardback, a large paperback and a large hardback. The two blue ones are both paperback, one small and one large. She doesn’t want the two blue ones next to each other. In how many ways can she do this?

Imagine a cube that’s turquoise on the front, pink on top, yellow on the right, white on left, dark blue on back and orange on the bottom. If Arne rotates this \(180^{\circ}\) about the line through the middles of the turquoise and dark blue sides, then does it again, he gets back to the original cube. If Arne rotates this \(90^{\circ}\) about that same line, then does that three more times, then he also gets back to the original cube.
Is there a rotation he could do, and then do twice more, to get back to the original cube?