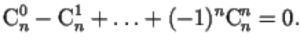Problems
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).
How many ways can you cut a necklace consisting of 30 different beads into 8 pieces (you can cut only between beads)?
30 people vote on five proposals. In how many ways can the votes be distributed if everyone votes only for one proposal and only the number of votes cast for each proposal is taken into account?
How many necklaces can be made from five identical red beads and two identical blue beads?
a) The sports club has 30 members, of which four people are required to participate in the 1,000 metre race. How many ways can this be done?
b) How many ways can I build a team of four people to participate in the relay race 100 m + 200 m + 300 m + 400 m?
How many ways can you build a closed line whose vertices are the vertices of a regular hexagon (the line can be self-intersecting)?
How many different four-digit numbers, divisible by 4, can be made up of the digits 1, 2, 3 and 4,
a) if each number can occur only once?
b) if each number can occur several times?
How many integers are there from 0 to 999999, in the decimal notation of which there are no two identical numbers next to each other?
Find the number of rectangles made up of the cells of a board with \(m\) horizontals and \(n\) verticals that contain a cell with the coordinates \((p, q)\).