Problem #PRU-98271

Problem

Imagine an infinitely large sheet of paper with a square drawn on it. Somewhere on the paper, a point \(P\) is marked with ink that is invisible to you. However, a friend with a special pair of glasses can see the point.

We are allowed to draw straight lines on the paper, and for each line, our friend will tell us on which side of the line the point \(P\) is. (If \(P\) is exactly on the line, they will say so.) For example, on this picture, our friend would say that the point \(P\) is above the line we’ve drawn:

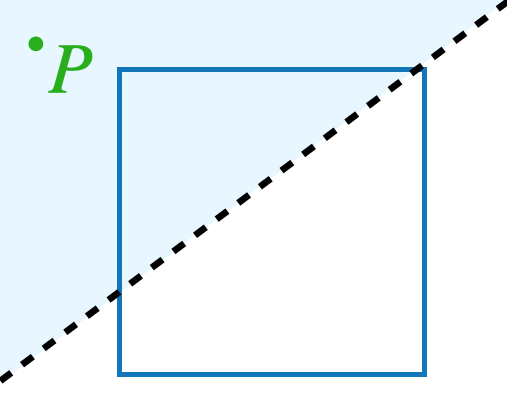
What is the smallest number of such questions that are needed in order to be certain whether \(P\) lies inside the square? Explain why it cannot be done in less questions then you are suggesting.