Problem #WSP-5302

Problem

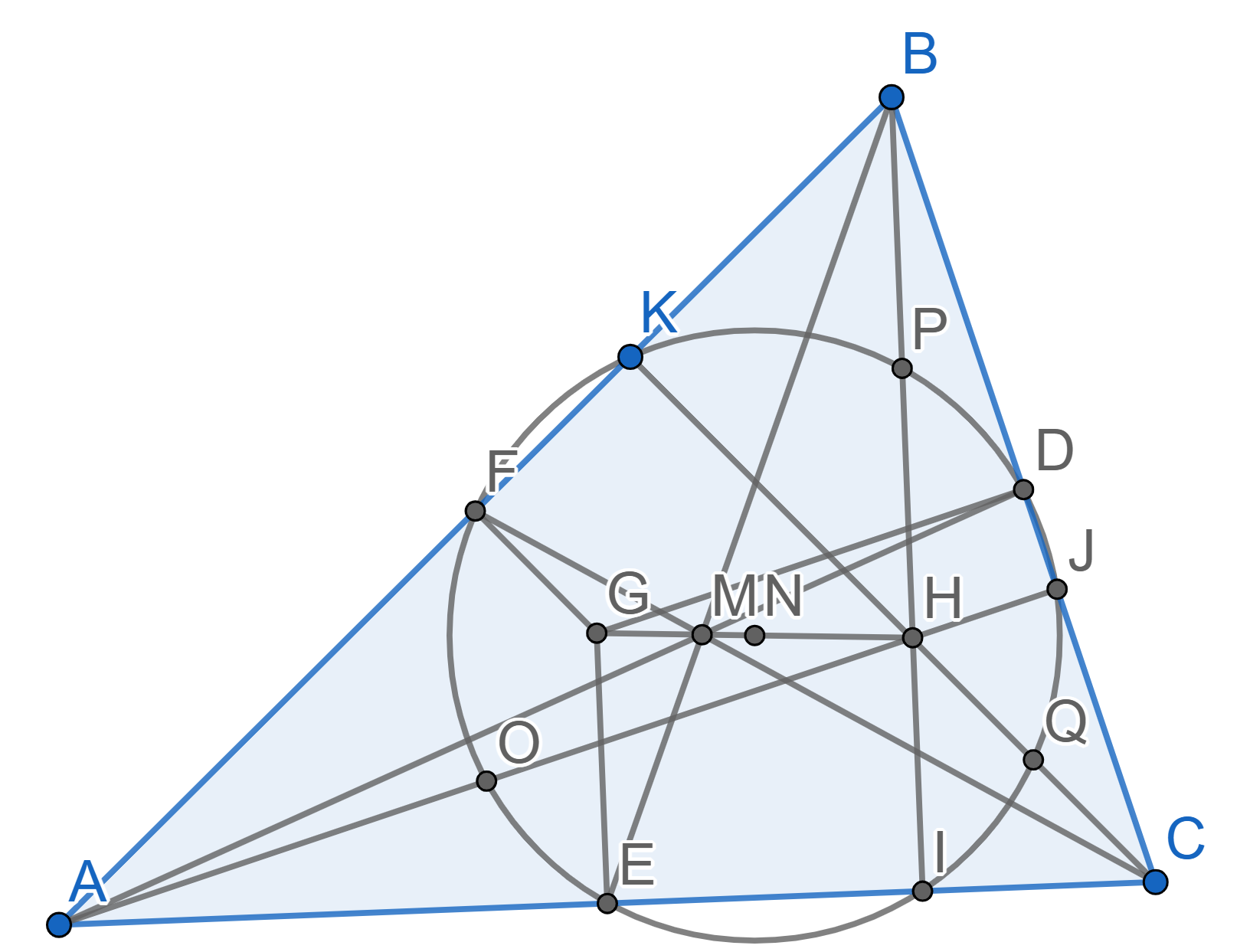
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Prove that the points \(D\), \(J\), \(I\), \(E\), \(F\) and \(K\) all lie on one circle.