Problem #WSP-00493

Problem

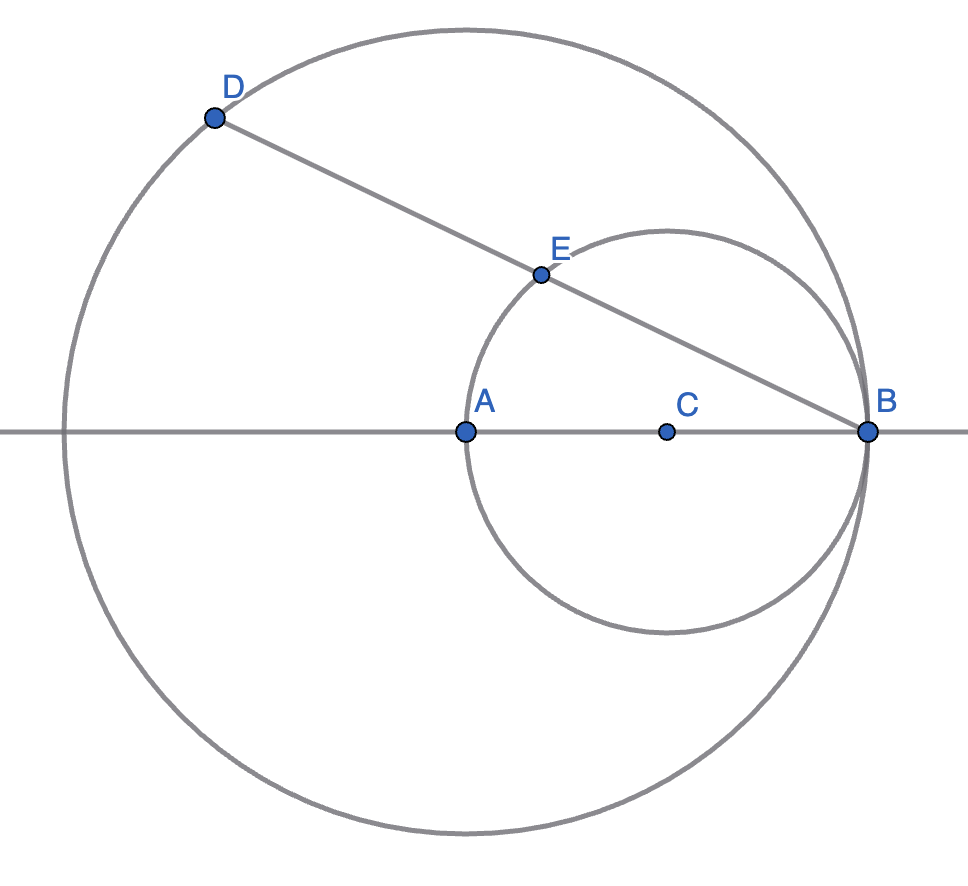
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (not \(B\)!) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.

Show that \(|BE|=|DE|\).