Problem #WSP-5568

Problem

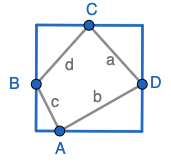
Four points \(A,B,C,D\) are chosen on the sides of a square of side length \(1\). The quadrilateral with vertices \(A,B,C,D\) has side lengths \(a,b,c,d\) as in the picture below. Show that \(2\leq a^2+b^2+c^2+d^2\leq 4\).