Problem #WSP-5579

Problems Game of Life
 11–12  2.0

Problem

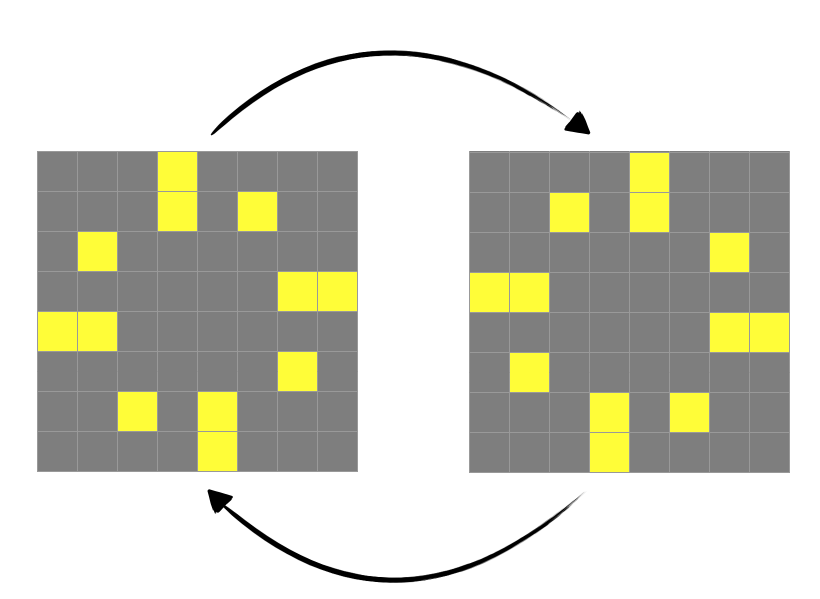
A phoenix is a pattern with the interesting property that all of its alive cells die after each generation, yet the pattern as a whole lives indefinitely. Show that if a phoenix is contained in some rectangle at the start, it can never extend more than once cell past this rectangle (i.e: a phoenix can’t expand forever). Below is a picture of a phoenix with period \(2\):

image