After login you will be able to create your own lists of problems.
Problems
Found: 21
Remember that two shapes are congruent if they are the same in shape and size, even if one is flipped or turned around. For example, here are two congruent shapes:

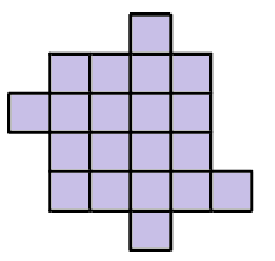
Cut the following shape into four congruent figures: