Problems
Today we will solve some logic problems. This time, we are visiting a strange planet. This planet is inhabited by two kinds of aliens, Cricks and Goops. The physical differences between them are not enough for a human being to distinguish them, but they have another remarkable feature. They can only ask questions. Cricks can only ask questions whose answer is yes, while Goops can only ask questions whose answer is no.
In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.
An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced “\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.
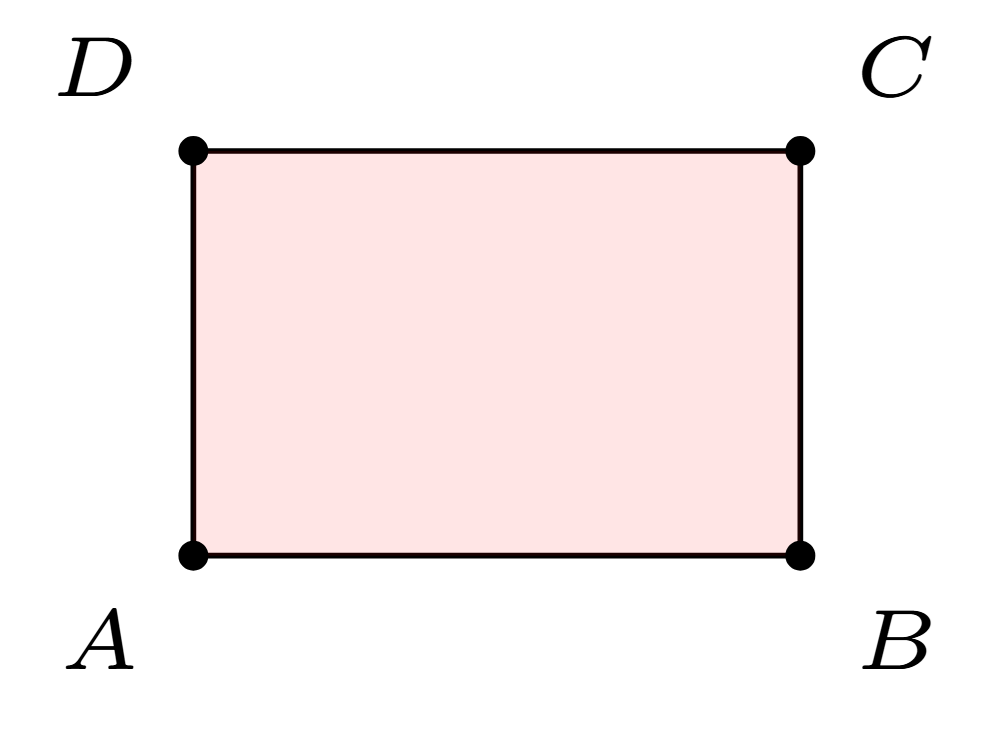
We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).
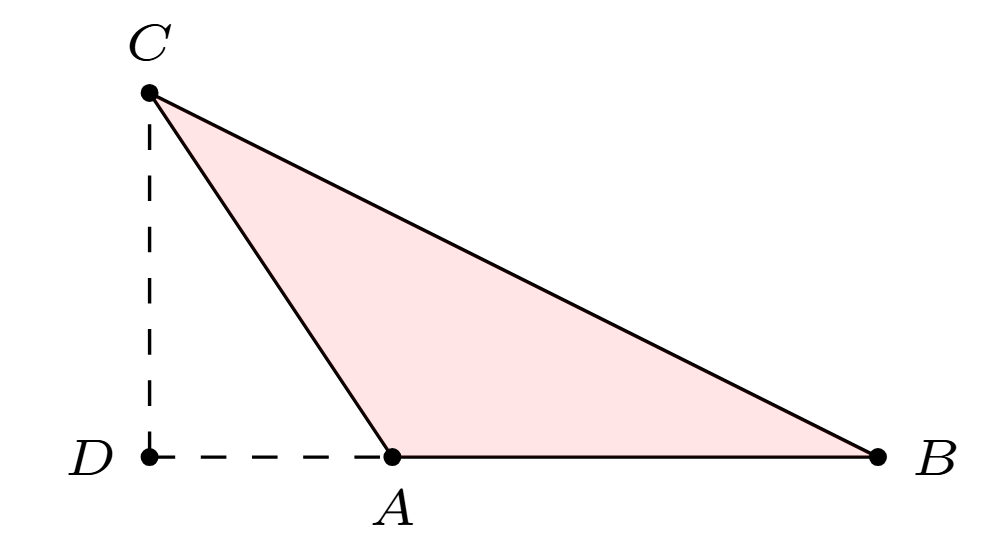
Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude.
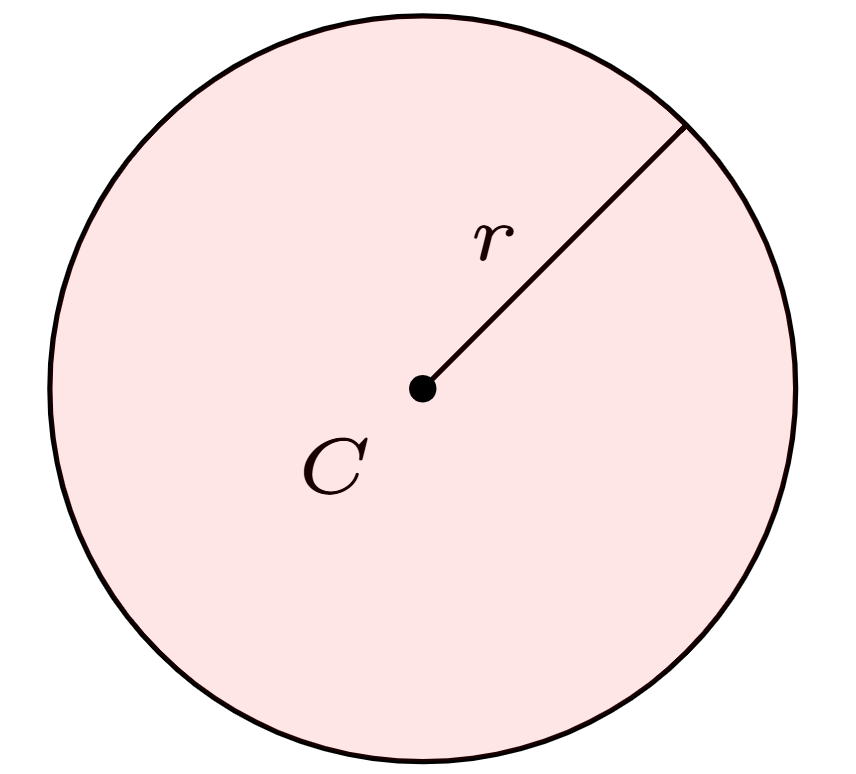
At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.
This week we’re looking at Fibonacci numbers, and other sequences of numbers.
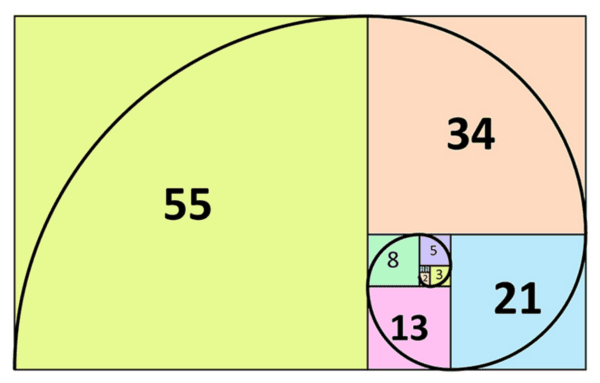
We say that the ‘zeroth’ Fibonacci number is \(0\) and the first Fibonacci number is \(1\). Then, from that point, every Fibonacci number is found by adding the two previous Fibonacci numbers. This means that the sequence begins \(0,1,1,2,3,5,8,13,21,34,55,89,144,...\)
The Fibonacci numbers hide lots of patterns which we’ll explore today. The spiral below is formed by taking squares whose side lengths are Fibonacci numbers, and drawing quarter circles in each square.
Prime numbers are like atoms that build every integer number. That is, a prime decomposition of a number is unique and then we can use it to find the number’s factors. Today we will explore this idea a bit more.
We will introduce a couple of new terms. First, a common divisor of two numbers is simply a number that both of these numbers can be divided by. Two numbers which have no common divisors (except from 1) are called relatively prime. We can establish if two numbers are relatively prime by looking at their prime factorizations - if they share no common primes, then they cannot share a common divisor!
Out of all the common divisors two numbers have, one must be the largest. This is an important number and is called the Greatest Common Divisor (GCD). You can find it by looking at the prime factorizations of the two numbers. For every prime number appearing in both factorizations, we take the smaller power. Then we multiply all our choices together. If we divide both numbers by their GCD, the resulting numbers will have no common divisors left and so will be relatively prime.
Similar to the notion of a common divisor is the one of common multiple. It is simply a number that is divisible by both numbers. Among the common multiples, one must be the smallest – this is called the Least Common Multiple (LCM). Again, the LCM can be found by looking at the prime factorizations of the two numbers. For every prime number appearing in any of the two factorizations, we take the larger power. Then we multiply all our choices together.
Today we will be looking at tilings. We define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated and symmetrical to each other. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that can be extended to cover the entire plane.
We will also look at some tilings of finite shapes, normally rectangles. You can imagine this as tiling a floor. With a huge number of \(1\times2\) tiles, we can investigate how to tile a floor in a rectangular room if no tile can overlap the other. It’s easy to tile the floor in a \(6\times8\) room.
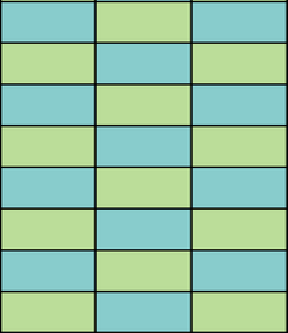
We can notice that if the floor in a room of size \(p\times q\) is tiled with \(1\times2\) tiles, then \(pq\) is even (can you explain why?). The reverse is also true; i.e. if \(pq\) is even, then the floor can be tiled with \(1\times2\) tiles in a similar way to the picture above.
However, this tiling can be cut from one side to another by a grid line without splitting any tiles. Such constructions are impractical, and this type of floor can easily become uneven. That’s why in practise irreducible tilings are used.
A tiling of a rectangle by small identical rectangles (tiles) is called irreducible if any straight cut from one side of the big rectangle to another goes across at least one of the tiles.
Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
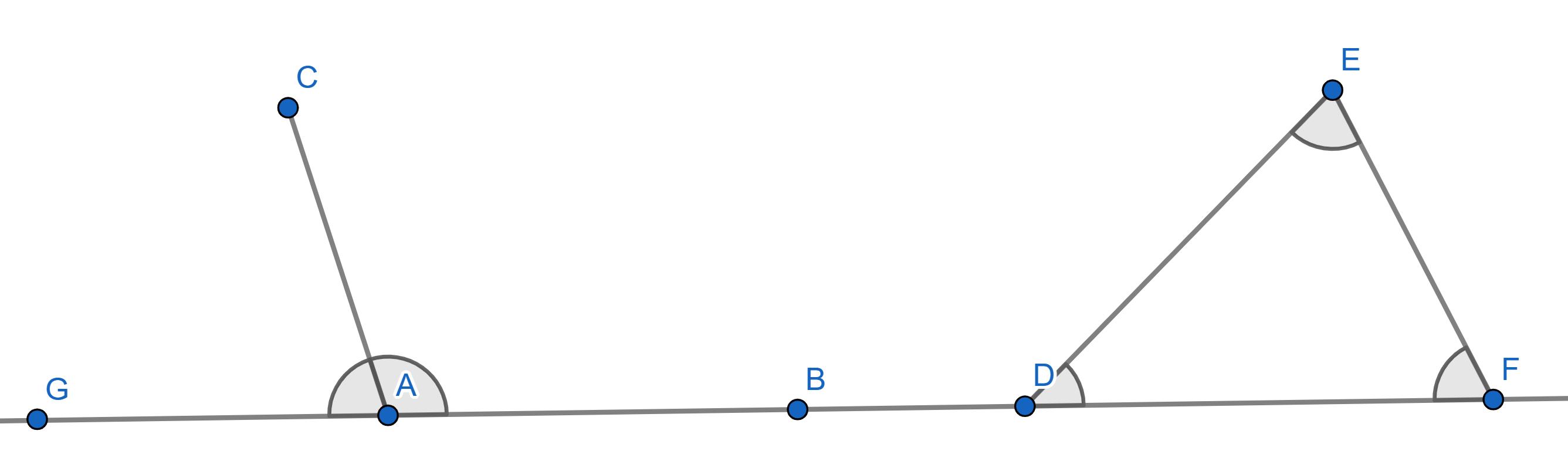
3. Two triangles are said to be “congruent" if ALL their corresponding sides and angles are equal.
We recommend solving the problems in this sheet in the order of appearance, as some problems use statements from previous problems as a step in the solution. Specifically, the inscribed angle theorem (problem 2) is required to solve every other problem that comes after it.
Just like atoms are the building blocks of molecules, prime numbers are the building blocks of integers, or whole numbers. What do we mean by this?
Well, every molecule is composed of atoms, and each atom is an atom of a particular element, like carbon or nitrogen. Similarly, every positive integer (except \(1\)) can be broken down into prime numbers. We can say this formally as follows:
The Fundamental Theorem of Arithmetic says that any natural number greater than \(1\) can be uniquely expressed as a product of prime numbers in non-decreasing order. For example: \[630=2\times3\times3\times5\times7=2\times3^2\times5\times7.\]
Recall that a number is composite if it is a product of two smaller, natural numbers. For example, \(6 = 2\times3\). Otherwise, and if the number is not equal to \(1\), it is called prime. The number \(1\) is neither prime nor composite.
Modulo operation: We look at division. For example \(41=2\times15+11\) is the division of \(41\) (the dividend) by \(15\) (the divisor) with remainder \(11\), and \(5=0\times7+5\) is the division of \(5\) by \(7\) with the remainder \(5\). More generally, when we divide \(a\) by \(b\), we’re looking for non-negative integers \(c\) and \(d\) (\(d<b\)) such that \(a=c\times b+d\).
In the case of \(45\) divided by \(15\), we get \(3\) with remainder \(0\) - in which case we say “\(15\) divides \(45\)", or “\(45\) is divisible by \(15\)". We can write this as \(15|45\).
We can deduce from the Fundamental Theorem of Arithmetic that if a product of two natural numbers is divisible by a prime number, then one of these numbers is divisible by this prime number. For example, \(7|7007=13\times539\) tells us that \(7\) divides \(13\) or \(539\). Clearly \(7\nmid13\), so we know \(7|539\).
It is often the case in geometric situations that figures look very similar, but not quite equal. Two polygons on a plane are called similar, if and only if ALL their corresponding angles are equal AND the ratio between ALL the corresponding sides is the same.
The relation between the corresponding sides, in our case it is \(\frac{AB}{IH}\) is called the similarity coefficient between the figures. It is common practice to write vertices of similar figures in the order that respects the similarity.
