Problems

Today we will have a look on some mathematical games. In all the games today, there are two players, who make moves alternately. There is a certain goal in each of these games, common for both players. The player who achieves it, wins, and the game will end at some point, draws are not allowed. It turns out in such games one of the players has a winning strategy - no matter what the other one does, the player following the strategy will always win. Today we can look into finding who has the winning strategy and what it might be.

One important tool we have to investigate these games are winning and losing positions. If you playing the game can win in one go starting from a certain state of the board, number of tokens on the table, set of cards etc, or whatever describes the current state of the game, it is said you are in a winning position. However, if all the moves you can make give the winning position to your opponent, it is said you are in a losing position. You must do a move that will guarantee you opponent to win - or at least give them a certain opportunity if they are smart enough to take it.

We can go further and say that a winning position is such a position that you can always make a move that will change the state of the game to the losing position for your opponent. Whereas a losing position is such a position that you must make a move that handles the winning position to the other player.

In some simple games the strategy can be guessed without going into details about winning or losing positions. But often you can start from the last stages of the game, find out what positions are immediately winning, then find all the losing positions that lead only there. In this way, working your way from the end of the game towards its beginning, one can characterize all the possible positions as winning or losing. The player that starts the game in a winning position has a winning strategy - if they start the game in a losing position, the strategy belongs to their opponent.

Mathematical Induction is a method to prove statements that are usually true for all natural numbers. The method consists of two steps.

• The first step, known as the base case, is to prove the given statement for the first natural number.

• The second step, known as the inductive step, is to prove that the true statement for the number \(n\) implies that the statement for \(n+1\) is also true.

To understand how the method of induction works we look at dominoes. Have you ever seen a line of dominoes falling? How does it happen?

To prove that a line of dominoes will all fall when we push the first one, we just have to prove that:

• The first domino falls down (base case)

• The dominoes are close enough that each domino will knock over the next one when it falls (inductive step).

DRAFT
We need to ensure that there isn’t overlap with the first areas problem sheet.
We can introduce the areas of a new shape, e.g. a trapezium more formally. Maybe an ellipse?

We’ll explore how to tile the plane using rectangles, more general quadrilaterals, pentagons and more unconventional shapes. In this exercise sheet, we define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated or reflected to one another. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that we see can be extended to cover the entire plane.

In the majority of today’s problems, one only needs to create a pattern for a small section of the plane, which can then be extended to cover the entire plane through repetition. Such tilings are referred to as periodic. Finding a tiling of the plane using identical shapes that is not periodic, meaning the pattern never repeats itself, has been a long-standing open problem. However, this problem was solved in an article published in March 2023 by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss. The idea of their solution is the following diagram from the article:

The hard part is to prove that this tiling is aperiodic.

You may have seen the pigeonhole principle before, sometimes called Dirichlet’s box principle. It says that if you have more pigeons than pigeonholes, and you put all of the pigeons into some pigeonhole, then there exists at least one pigeonhole with at least two pigeons. While it sounds quite simple, it’s a powerful technique. The difficult thing is often choosing the appropriate pigeons and pigeonholes.
It has multiple applications in various situations.
Today we will see how to use it in geometric problems.

Sometimes it is hard to rigorously formulate an intuitively correct reasoning. We might not know the proper words, the proper language, we might not have the right tools. Maths problems are not an exception. When we start learning to solve them, we know nothing about possible mathematical approaches and mathematical models. Today you will learn a very useful way to visualise information: you will learn how to represent information as a graph.

A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges.

In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, etc, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes, etc. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.

Today we will solve some problems involving counting the same quantity twice (or more times) in different ways, which will let us learn about the components making it up.

A remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\).

More generally, given any integer \(n\) and positive integer \(k\), we can always write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more. This means we can always enforce the condition \(0\leq r<k\) on the remainder \(r\).

The general rule is that the remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) leaves the remainder \(3\) when divided by \(7\) and \(11\) leaves the remainder \(4\) when divided by \(7\). The product \(10\times11=110\) has the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then calculate the remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder of \(5\) when divided by \(7\). We can verify the result by calculating the remainder without simplifying first: \(110=15\times7+5\).

Here is a useful notation when discussing problems involving remainders and divisibility although it is not necessary for this problem sheet. Take two integers \(a\) and \(b\). If they differ by a multiple of a positive integer \(k\), then we write \(a \equiv b \pmod{k}\). For example, since \(24 - 10 = 2 \times 7\), we can express this fact by \(10 \equiv 24 \pmod{7}\). We say that 10 and 24 are congruent modulo 7.

Using this new notation, we can easily express the rules for remainders. Let \(a \equiv b \pmod{k}\) and \(c \equiv d \pmod{k}\). Then we have \(a + c \equiv b + d \pmod{k}\) and \(a \times c \equiv b \times d \pmod{k}\). As an example, again consider the calculation of the remainder of \(10 \times 11\) when divided by 7. We have \(10 \times 11 \equiv 3 \times 4 \equiv 12 \equiv 5 \pmod{7}\).

We make one last observation, which shows the utility of remainder when discussing divisibility. Saying that a number \(a\) is divisible by a number \(k\) is the same as saying the remainder of \(a\) when divided by \(k\) is 0. In congruence notation, the latter condition is \(a \equiv 0 \pmod{k}\).

Let’s have a look at some examples with remainders:

As the title suggests, today we’re going to colour some (if not all!) points in the plane, using only a couple of colours. We’ll show that no matter how we do this colouring, we’re guaranteed to get some structure. When we say ‘the plane’, imagine a flat piece of paper extending infinitely far in every direction.

Let’s look at some examples!

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

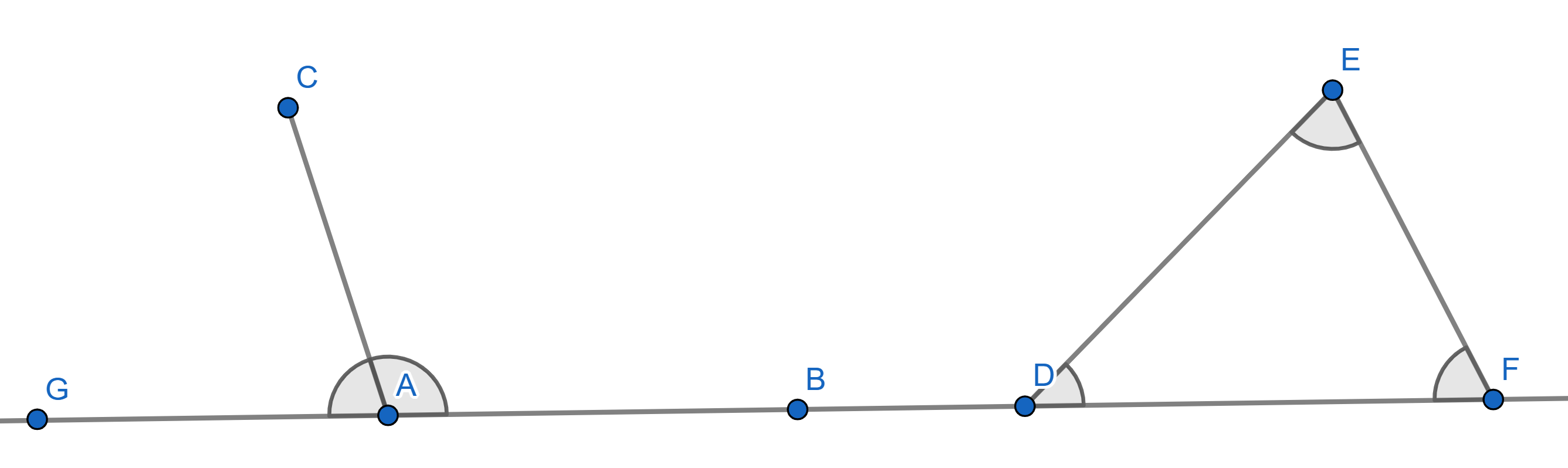
3. Two triangles are said to be “congruent" if ALL of their corresponding sides and angles are equal.
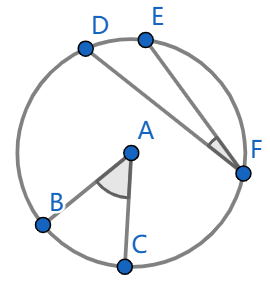
The following terminology will also be quite helpful. In the picture below, the points \(B\) and \(C\) lie on the circumference of the circle while the vertex \(A\) lies at the centre of the circle. We say that the angle \(\angle BAC\) is a central angle. The angle \(\angle DFE\) is called an inscribed angle because the vertices \(D\), \(F\) and \(E\) all lie on the circumference of the circle.